/*
This file belongs in
<TheGHOUL/DemoFiles/>
Hank J. van Leuvensteijn Jr. 2021
theghoul@hankjr.ca
*/
include<TheGHOUL/Config.scad>
/*
For good looks, $fn=360; things will be slow... For testing and 'okay' looks, $fn=60 is dandy.
*/
$fn=360;
/* Set the viewport and animation. */
$vpt=[0,0,0];
/*
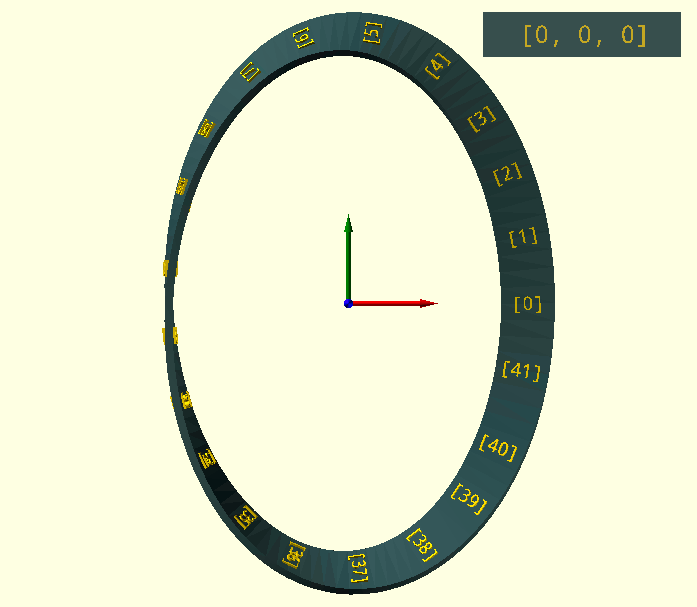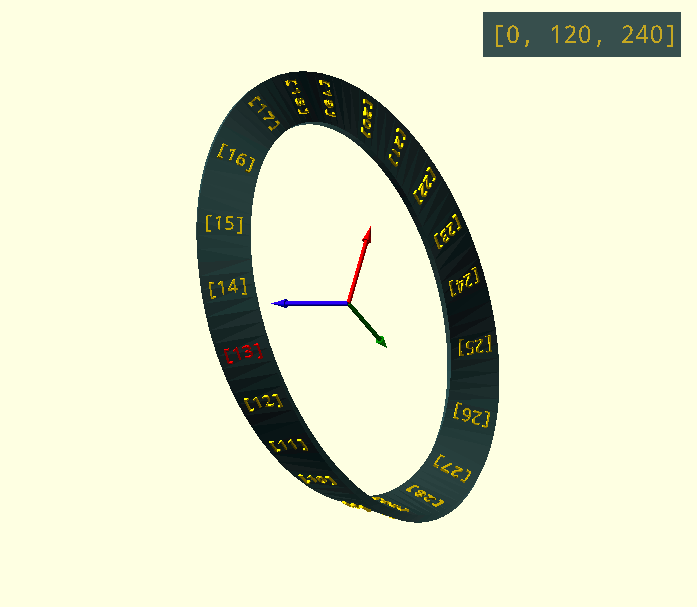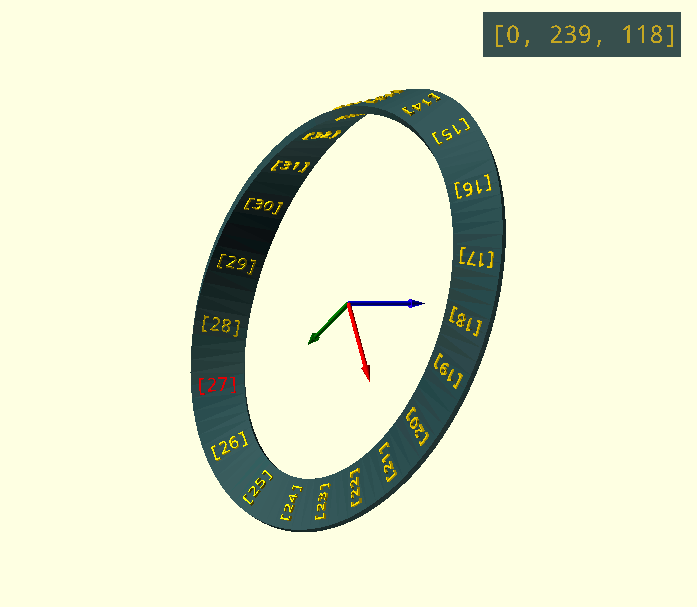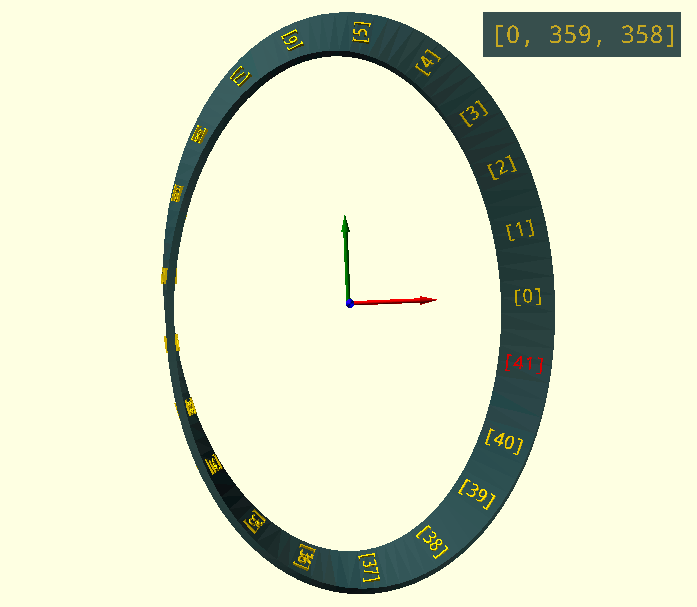
Animation is a simple viewport rotation; two Z-turns to see the entire surface (two sides!) of the Möbius band with a single simultaneous Y-turn to keep the current 'Index' facing the viewer.
*/
$vpr=[0,0+$t*360,$t*720];
$vpd=170;
/* Parse the rotation angles for display, yes, $vpr.x=0... */
vpr=[round($vpr.x%360),round($vpr.y%360),round($vpr.z%360)];
/* Set a few parameters. */
Width=6;
Thickness=0.9;
/* Pad a 2D ellipse vertex array to 3D. */
Elly=PadArray(Ellipse(20,30,true)[0]);
TotalVertices=len(Elly);
TVS=TotalVertices-1;
/*
A Möbius band makes a 180 degree twist in one full turn, connecting the 'outside' surface to the 'inside' surface, thus eliminating both and creating a single surface.
Generate an array with JUST the offset vectors to width/2.
For each two successive vertices in the ellipse, an offset vector, perpendicular to the curve and in the Z=0 plane (the plane of the ellipse) is rotated over an angle proportional to the current vertex number over the total number of vertices.
*/
Welly=[ for(I=[0:TVS])
AffineTransformVertex(
RotationMatrix(
/* Rotation axis is vector between current vertex and the previous. Of course I'm using MoebiusArray() here, but you'd use Dex(). */
MoebiusArray(Elly,I+1)-Elly[I],
/* Rotation angle is proportional to vertex number. */
I/(TVS+1)*180
),
/* The offset vector is perpendicular to the curve in Z=0 plane. */
LPerpVector(MoebiusArray(Elly,I+1)-Elly[I],Width/2)
)
];
/*
As above, but now rotate a small vertical (i.e. perpendicular to the width-offset vector) vector representing thickness/2. See above for comments.
*/
Telly=[ for(I=[0:TVS])
AffineTransformVertex(
RotationMatrix(
MoebiusArray(Elly,I+1)-Elly[I],
I/TVS*180
),
[0,0,Thickness/2]
)
];
/*
Add and subtract the above created offset arrays to the original ellipse vertex array to generate the 4 curves forming the 4 corners of the band cross-section.
*/
Belly=[for(I=[0:TVS]) Elly[I]+Welly[I]-Telly[I]];
Helly=[for(I=[0:TVS]) Elly[I]-Welly[I]-Telly[I]];
Jelly=[for(I=[0:TVS]) Elly[I]-Welly[I]+Telly[I]];
Kelly=[for(I=[0:TVS]) Elly[I]+Welly[I]+Telly[I]];
/* Concat all vertices. */
Vertices=concat(Belly,Helly,Jelly,Kelly);
/*
Define bottom, side and top faces and stitch the ends together. Faces have four corner vertices, a pair from two adjoining curves each.
*/
Faces=[
for(I=[0:TVS-1])
[I,I+TotalVertices,I+TotalVertices+1,I+1],
for(I=[0:TVS-1])
[I+TotalVertices,I+2*TotalVertices,I+2*TotalVertices+1,I+TotalVertices+1],
for(I=[0:TVS-1])
[I+2*TotalVertices,I+3*TotalVertices,I+3*TotalVertices+1,I+2*TotalVertices+1],
for(I=[0:TVS-1])
[I+3*TotalVertices,I,I+1,I+3*TotalVertices+1],
/* Closing faces are not regular as one end has made a 180 degree rotation. Stitch them together explicitly. */
[3*TotalVertices-1,4*TotalVertices-1,1*TotalVertices,0],
[4*TotalVertices-1,1*TotalVertices-1,2*TotalVertices,TotalVertices],
[1*TotalVertices-1,2*TotalVertices-1,3*TotalVertices,2*TotalVertices],
[2*TotalVertices-1,3*TotalVertices-1,0,3*TotalVertices]
];
/* Calculate spacing. */
PStep=(CurveLength(Helly,true)+CurveLength(Belly,true))/43;
/*
Generate the text. Because the vertices on the elliptical path are not equidistant, selecting vertices by number doesn't work (the text looks funky because the distance between consecutive numbers looks uneven) instead, we need to select vertices by position on the curve, i.e., distance.
*/
for(I=[0:41]){
Vertex=FindCurveVertex(Elly,I*PStep,true);
/* We need two points for a rotation vector. */
Node1=MoebiusArray(Elly,Vertex);
Node2=MoebiusArray(Elly,Vertex+1);
Vector=Node2-Node1;
/* The rotation is proportional to vertex number over array length, like above. */
Roll=Vertex/TotalVertices*180;
/* Give the 'currently viewer facing' (ish) index some colour. */
color(((I)/42<=$t&&(I+1)/42>$t)?"red":"gold")
/* Place the text. */
Position(Vector=Vector,Base=Node1,Roll=Roll)
/* Align text with +Z-axis for Position(), above. */
rotate([90,0,-90])
/* Small correction to center text and raise it above the band surface. */
translate([-0.15,0,0.2])
SimpleText(str("[",I,"]"),1.5,Thickness=0.5,Center=true,Font="Noto Mono",Spacing=0.8);
}
/* Generate the Möbius band. */
color(DSG)
polyhedron(Vertices,Faces,5);
/* Visualise the coordinate system. */
CoordinateSystem(Size=10,Thickness=0.5,Points=[0,0.2,1],Polar=false);
/* Put some info in the picture, compensate for viewport rotation to keep text facing torward the user during animation. */
rotate($vpr)
/* Put it in the top-right corner. */
translate([26,30,0])
{
/* Put the square behind the text. */
translate([0,0,-1])
color("darkslategrey",0.7)
square([22,5],center=true);
/* Show rotation angles. */
SimpleText(str(vpr),Size=2,Thickness=0.2,Center=true,Font="Noto Mono",Spacing=0.8);
}