Nothing happens until something moves.
— Albert Einstein

Using animation.

Let’s get this out of the way first: OpenSCAD isn’t POV-Ray or Blender or Animaker or what-have-you, but sometimes it’s just nice to have stuff move, or change colour, or zoom in or…​ Well, that’s what the animation view is for, but it’s not too user-friendly. Enter: The Animation.scad library…​ (Far from perfect or finished…​)

Bezier Vase

OpenSCAD provides the special variable $t which grows in linear fashion from 0 at the beginning of the animation sequence to 1 at the end. It provides therefore a fraction of the entire sequence, which can be used to create animations by directly incorporating it in an object’s call.

Say we want to create a 15 second animation sequence. We want a cube that becomes visible at 3 seconds and disappears at 7 seconds. We also want it to be transparent at the start, fully opaque at 5 seconds,and transparent again just before it disappears:

if ($t>0.2&&$t<0.467)
    color("red",0.3+0.7*pow(sin(($t-0.2)/(0.467-0.2)*180),2))
    cube([1,1,1]);

It requires a fair understanding of math, and some serious bookkeeping of your start and end factors. An additional problem is that when the total length of the animation changes, all factors for $t also need to change. Hmmm, not much 'parametric' about that. Of course you can do:

Length=15;
CStart=3;
CEnd=7;

if ($t>CStart/Length&&$t<CEnd/Length)
    color("red",0.3+0.7*pow(sin(($t-CStart/Length)/(CEnd-CStart)/Length*180),2))
    cube([1,1,1]);

Mostly parametric and kind of 'more better' to speak with Capt. Jack Sparrow, but it’s still ugly code, and if you have several animated objects, keeping track of all the factors gets old very quickly.

Or you can use one of the routines in this library, for example Animate() like so:

$AnimSegs=15;
Animate([1,3,7,7])
color("red",$AnFlash)
cube([1,1,1]);

The vector parameter given to Animate() is an AnimVector, a vector that describes when something (an object or property) is created, begins to change, stops changing, and when it stops being, in seconds or minutes, or whatever time unit you prefer. Nice and easy. Have a cuppa.
Animate() provides special variables to it’s children() to influence colour, position, rotation, you name it, we’ll see them in a moment.

Addressing time in The GHOUL’s animation library.

All animation routines in The GHOUL rely on $AnimSegs. It is the number of segments in the animation. 'Segment', here, means 'time unit'. Usually, for short animations, a segment will be equal to one second, but for longer animations it may be interpreted as one minute; it’s whatever you prefer; if you like working in 3 second segments, it can mean that…​ $AnimSegs enables you to address time-points in the animation with 'human-friendly' numbers, like 5 seconds, instead of the fractions of the total duration of the animation that $t requires, like $t=0.333 for when something has to happen at 5 seconds into a 15 second animation.

It also allows you to change the duration of the animation, without having to rewrite all the fractions. Mighty dandy.

$AnimSegs=15; // Total animation lasts 15 seconds.

$AnimSegs MUST be declared in your main (top level) file so it is available to all animation routines. For convenience, (since it’s a Special Variable anyway) The GHOUL’s configuration file config.scad already contains the declaration $AnimSegs=10;.

IMPORTANT:

The Animation view in OpenSCAD View › Animate has two settings: Steps and FPS. Let’s say you want 15 seconds of animation at 10 Frames Per Second, then you will need 10 FPS x 15 Seconds = 150 Steps.

In the above example we would want to declare $AnimSegs=15; for one second per animation segment.

What if you need to extend the sequence to 20 seconds instead of 15? Simply set $AnimSegs=20; and Steps = $AnimSegs x FPS = 20 x 10 = 200. Easy, and the animations that are already defined will be unaffected in real time because each segment still lasts one second. I told you; dandy.

Important Whenever the word 'Frequency' is used on this page, it has the meaning of the first dictionary entry, i.e., 'occurances or repetitions over a period of time', and not that of the second entry, i.e., 'cycles per time unit'. The main distinction being that the first, which we’re using here, deals with 'periods of time' of any length, and the second with time divided in distinct, equal length units, like in Hertz, or CPS &c.
More explicitly, 'Frequency' here means 'do this completely, X times, spread out evenly over the entire animation period'.

To further clarify, 'animation period' here means the time period over which an object changes it’s shape, location or appearance, not the time it exists, or the time covered by the entire animation, i.e., $t=0 to $t=1.

Animate()

Animate(AnimVector=[Create,Start,Finish,Delete],Frequency=1)

  • AnimVector, a vector of times, determining the state of children():

    • Not yet displayed. (t < Create)

    • Displayed in initial form. (Create < t < Start)

    • Displayed and changing. (Start < t < Finish)

    • Displayed and no longer changing. (Finish < t < Delete)

    • No longer displayed. (Delete < t)

  • Frequency, the frequency of periodic special variables returned by Animate(), explained in depth below.

This routine generates a variety of special variables that are available to children() to change their size, color, orientation or location. Let’s for a moment look at that cube from earlier, this time in a shorter 4 second animation:

$AnimSegs=4; // Total animation lasts 4 seconds.
Animate([0.5,0.5,3.5,4])
color(RED,$AnFlash)
cube([1,1,1]);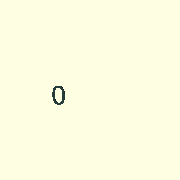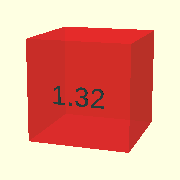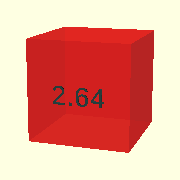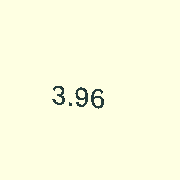

Animated Cube

The AnimVector determines that the cube is created and becomes visible at 0.5 seconds into the animation, develops until 3.5 seconds into the animation and disappears at 4 seconds. The special variable $AnFlash is used as the alpha fraction for color(). $AnFlash returns a sinusoid curve that starts at 0, increases to 1.0 and decreases to 0 again. Animate() forces the curve to fit exactly in the lifespan of it’s children() so at 0.5 seconds the cube has alpha=0, at 2 seconds alpha=1.0 and at 3.5 seconds alpha=0 again.

These are the special variables Animate() provides to manipulate its children():

  • $AnBump: Starts at 0, bumps against 1.0, dips to 0.8 and grows back to 1.0. Use for height of a cylinder.

  • $AnBounce: Starts at 0, overshoots to 1.3, drops back to 1.0. Use for radius of a sphere.

  • $AnAlpha: Starts at 0.3, has a short delay and smoothly increases to 1.0. Use for alpha to make an object appear smoothly.

  • $AnOmega: Starts at 1, has a short delay and smoothly decreases to 0.3. Use for alpha to make an object disappear smoothly.

  • $AnFlash: Starts at 0, increases to 1.0 and decreases to 0 again. Use as alpha or in a color vector to highlight an object temporarily.

  • $AnFlashing: Like $AnFlash, but keeps cycling after maturity. Cycling speed is determined by Frequency.

  • $AnDip: The opposite of $AnFlash; starts at 1.0, dips to 0.3 and goes back to 1.0.

  • $AnWobble: A sinusoid between 0 and 1, starts at 0.5.

  • $AnTrngl: Continuous triangular wave signal between 0 and 1.0, uses Frequency.

  • $AnFrac: Continuous saw-tooth wave signal between 0 and 1.0, uses Frequency.

  • $AnSqr: Continuous 'square wave' (flip-flop) signal between 0 and 1.0, uses Frequency.

Here are some examples:

Animated Sphere

A sphere that bounces past it’s final size and comes back:
Animate([0,0,2,4]) sphere(r=$AnBounce*5);

Animated Cylinder

A cylinder that bumps against it’s final size and grows back:
Animate([0,0,2,4]) cylinder(r=1, h=$AnBump*2);

Animated Cube

A cube that rotates back and forth over 180 degrees:
Animate([0,0,2,4]) rotate([0,0,$AnPulse*180]) cube([1,1,1]);

The possibilities are endless. Probably.

Animator()

Animator(StepArray,Shift=0)

  • StepArray, array, an array of time-value pairs.

  • Shift, time-period, a period in $AnimSegs segments (seconds, minutes, what-have-you) to 'shift' the animation events of this parameter.

Note Perhaps it’s obvious, but in the following paragraphs, TimeNow has the meaning of 'the current time in the animation'.

Whereas Animate() provides some nice pre-made functions, and also a pretty customisable one, if you need a succession of changes for a specific parameter, Animator() is your guy. It allows you to specify a list of times and values for your parameter to 'walk through' during the animation, here’s an example of StepArray:

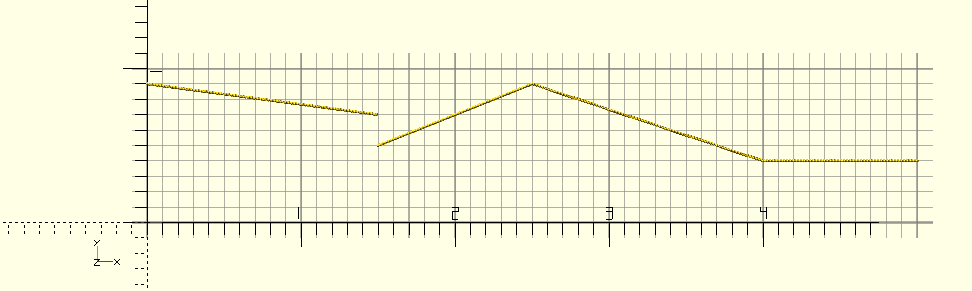
[[0,0.9],[1.5,0.7,0.5],[2.5,0.9],[4,0.4],[5,0.4]]

Of each element, the first item is a Time, and the second item is the Value for the parameter at that time (we’ll get to the third in a minute). At every step during the animation, Animator() looks for the last Time previous to TimeNow, i.e., $t*$AnimSegs, and returns the interpolated value between this [Time,Value] pair and the next one, since TimeNow lies between these two.

[Time,Value1(,Value2)]

  • Time, strictly: a time-point in $AnimSegs, probably in seconds.

  • Value1, scalars, lists of scalars (like a rotation [30,0,45]) or strings. Obviously, in the case of a string, there’s no interpolation, the TimeNow string is used.

  • Value2, (optional and usually absent), if this value is given,the resulting signal will step instantaneously, at exactly Time, from Value1 to Value2, and then keep changing proportionally, as per, from there.

When TimeNow lies outside the time-range covered by StepArray, i.e. is smaller than the first or larger than the last time-point, the respective value will be used, that is, the first value when TimeNow is earlier than the first Time, and the last when it’s later than the last.

Animator Graph

Shift is a value in segments (see $AnimSegs above), added to TimeNow to enable shifted transitions, i.e. transitions in one variable, let’s say colour, are phase-shifted from transitions in another variable, say diameter, of an object. To properly use this, you should define StepArray up to $AnimSegs+Shift.

Let’s have a quick peek at the example again:

Foo=Animator([[0,0.9],[1.5,0.7,0.5],[2.5,0.9],[4,0.4],[5,0.4]]);

What’s going on here?

Time       Foo
0          Starts at 0.9
0...1.5    Decreases proportionally to 0.7
1.5        Steps to 0.5
1.5...2.5  Increases proportionally to 0.9
2.5...4    Decreases proportionally to 0.4
4...5      Remains at 0.4 (actually, changes from 0.4 to 0.4)

Notice especially what happens at the second element. The signal converges to it’s first value of 0.7, and at it’s time of 1.5, the signal steps to it’s second value of 0.5 and continues to change from there…​

Cycle()

Cycle(Min=0,Max=1,Frequency=1,Start=undef)

  • Min, Max, scalars, tuples, vectors, vertices; limits.

  • Frequency, scalar, cycle frequency.

  • Start, start-value.

Cycle() cycles—​predictably—​between two values, at a given frequency, starting at the lower value—​unless a start-value is specified—​over the [0…​$t] interval. It can be used for any cyclic changes in location, rotation, even colors.

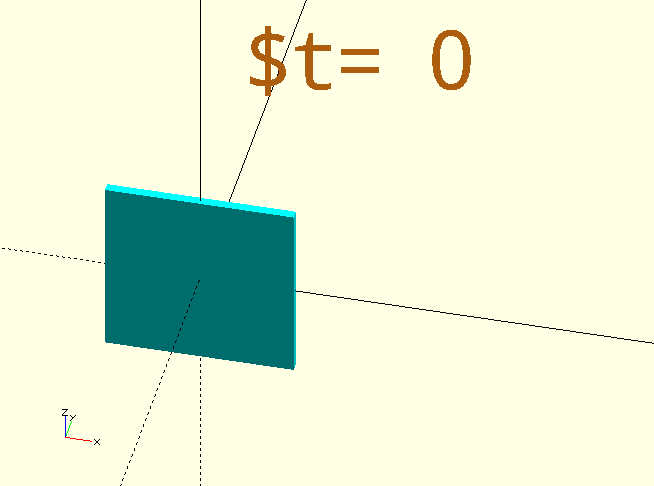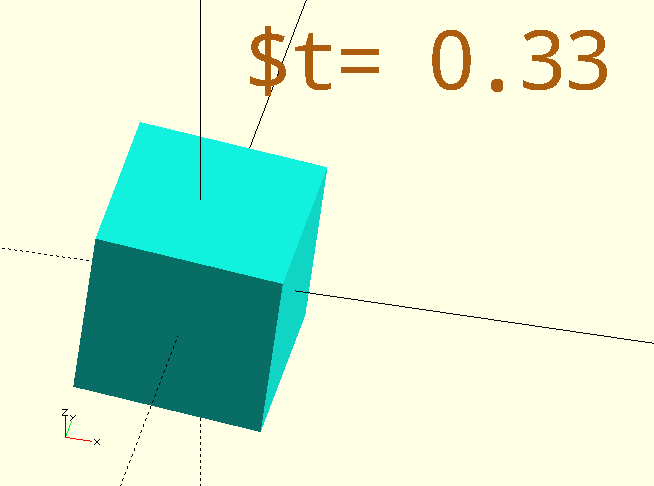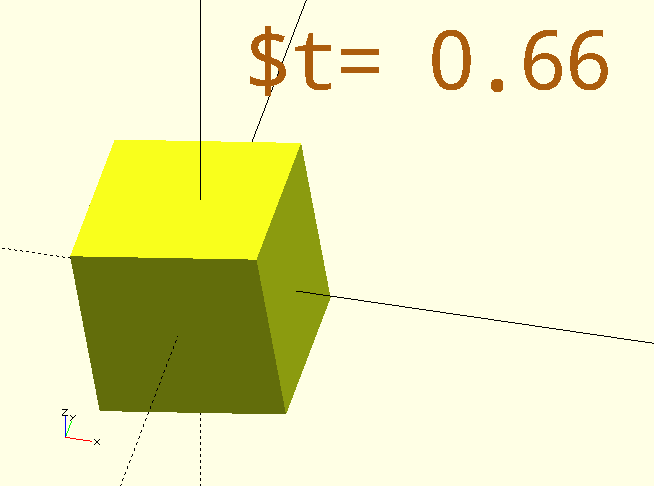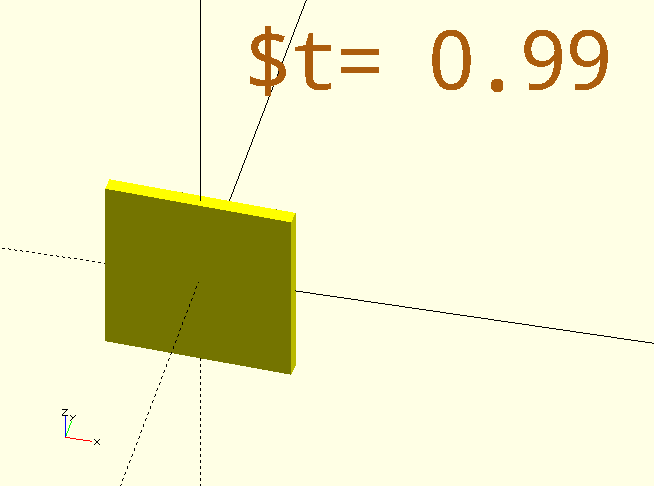
StringTee

StringTee()

Animate() or Animator() may be a bit more than you need, in which case The GHOUL offers StringTee() as a simpler option, at the price of some more 'book-keeping'.

The function

StringTee(Start,Finish,BeginValue,EndValue)

  • Start, time, when to start the animation

  • Finish, time, when to finish the animation

  • BeginValue, scalar, value of StringTee() before the beginning of the animation

  • EndValue, scalar, value of StringTee() at the end of the animation

A more 'rough and ready' approach to animation, StringTee() provides a simple command to quickly generate an interpolated value between two time-points (see $AnimSegs above). This value can be used to change an object’s position, rotation, color, size, whatever you like. Note that with StringTee() the object always exists, unlike with Animate(), where an object can appear and disappear at any time, unless…​ you use the module (see below).

Here’s what happens:

Time Parameter

Before Start

Equal to BeginValue

Between Start and Finish

Proportional from BeginValue to EndValue

After Finish

Equal to EndValue

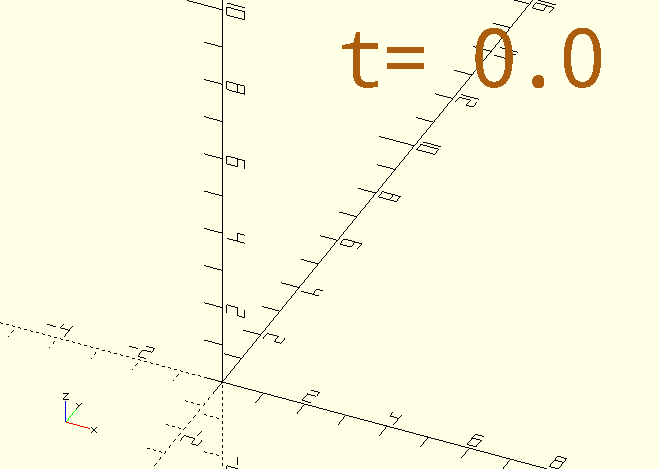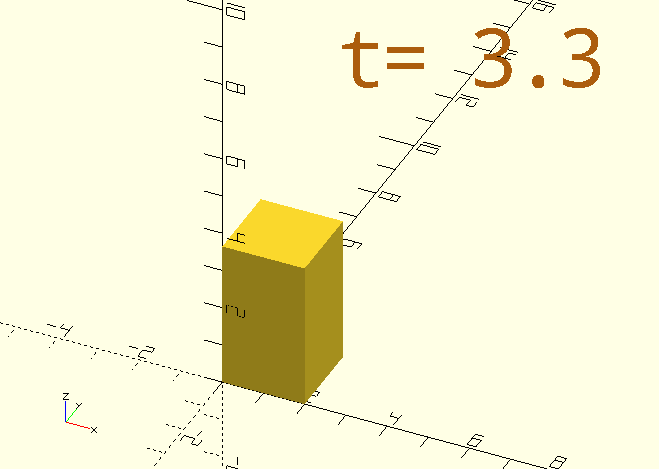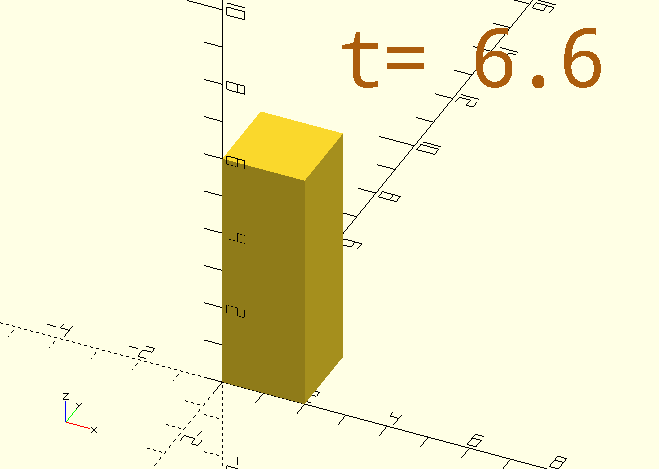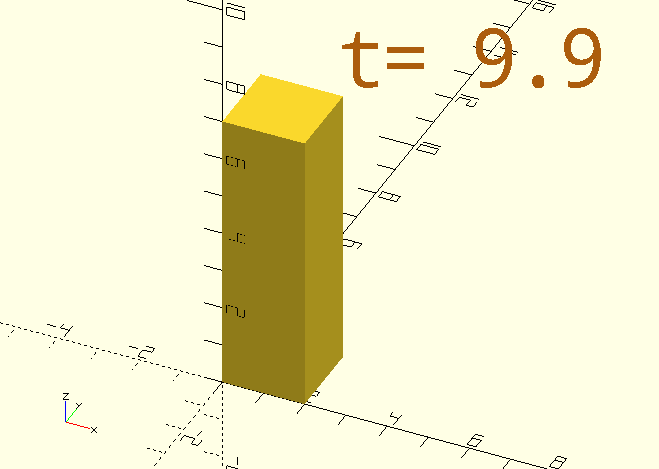
Here’s the code for that funky-rotating-colour-shifting cube in the image:

$AnimSegs=10;

color([StringTee(3,7,0,255)/255, 255/255, StringTee(3,7,255,0)/255])
rotate([StringTee(0,3,0,90),StringTee(3,7,0,90),StringTee(7,10,0,90)])
// Notice the 'stacked' calls to make the cube's dimension increase and then decrease again.
cube([20,StringTee(0,3,1,20)-StringTee(7,10,0,19),20],center=true);

color(CPR)
ScreenPosition(Location=[-3,5,0])
SimpleText(str("$t= ",$t),2,Spacing=0.75);

If direct proportionality isn’t good enough, you can get a little more sophisticated with something like this:

$AnimSegs=10;
// Changes from 0 to 1 with 'soft' start and end.
SoftUnit=(cos(StringTee(2,8,180,360))+1)/2;

translate([SoftUnit*10,0,0])
cube([2,2,2]);

However, if that’s what you wanted, you should probably be using BezierTransitionUp()…​

StringTee

The module

StringTee(Start,Finish,BeginValue,EndValue,Preexisting=false,Enduring=true)

  • Start, time, when to start the object animation.

  • Finish, time, when to finish the object animation.

  • BeginValue, scalar, value of StringTee() before the beginning of the animation

  • EndValue, scalar, value of StringTee() at the end of the animation

  • Preexisting, Boolean, if true, the oject(s) will exist from $t=0.

  • Enduring, Boolean, if true, the oject(s) will persist until $t=1.

Wait. StringTee() also has a module? Yes, and unlike the function, the module regulates the existence of children() similarly to Animate(), and, similar to that function, it supplies a special variable, $StValue, to it’s children. $StValue is simply that which is returned by the StringTee() function, the module simply adds functionality like `Animate()’s Start and Finish &c, through it’s Preexisting and Enduring parameters. The object only exists between Start and Finish, unless either of the boolean parameters is true.

$AnimSegs=10;
StringTee(1,8,2,7,false,true)
cube([2,2,$StValue]);

If you’d like to take your viewers on a 'flying tour' around your objects, The GHOUL offers Viewport():

ViewPorts

ViewPort()

ViewPort(ViewPorts)

  • ViewPorts, array of ViewPort definitions. Each definition takes the form of
    [Time,$vpt,$vpr,$vpd] where:

    • Time is a time-point in the animation. Time must start at 0 and go up to $AnimSegs, and successive time-points must be in increasing order (time is funny like that), as ViewPort() uses the Time parameters to interpolate between the successive ViewPorts. ViewPort() divides the animation sequence ($t=0 to $t=1) over $AnimSegs time units, and interpolates the successive ViewPorts linearly, proportional to their Time parameters on this interval.

    • $vpt, $vpr and $vpd, are well documented in the OpenSCAD manual entry.

ViewPort() is probably my favourite of The GHOUL’s animation functions. Just define a few nice ViewPorts, and it takes you on a journey of zooms, translations and rotations around your objects.

To 'stand still' at a ViewPort, simply repeat it in the list, say you want to stop at the second ViewPort for a while; the list will look like this: [[ViewPort1],[ViewPort2],[ViewPort2],[ViewPort3],…​] and the Time-s could be something like: 0,1,4,5,6…​ Now you will look at [ViewPort2] from Time=1 till Time=4.

If two ViewPorts are 180 degrees offset, consider the direction of rotation. Going from [0,0,180] to [0,0,0] is opposite to going from [0,0,180] to [0,0,360]. OpenSCAD doesn’t care how big you make the angles; want to keep turning the same way? Just keep increasing the angle.

Viewports example.
// Can't do a thing without:
include<TheGHOUL/Config.scad>

// Declare some ports:
MyView=ViewPort([
    [0,[0,0,0],[60,0,45],25],
    [1.0,[0,0,0],[60,0,90],200],
    [3.0,[0,0,0],[135,0,225],200],
    ...
    [7.0,[0,0,0],[90,0,270],100],
    [9.0,[0,0,0],[90,0,0],150],
    [12.0,[0,0,0],[60,0,45],25]
]);

// Move the world:
$vpt=MyView.x;
$vpr=MyView.y;
$vpd=MyView.z;

// Something to look at...
cube([20,20,20]);
color("red")
sphere(r=10);

More control? You’ve got it!

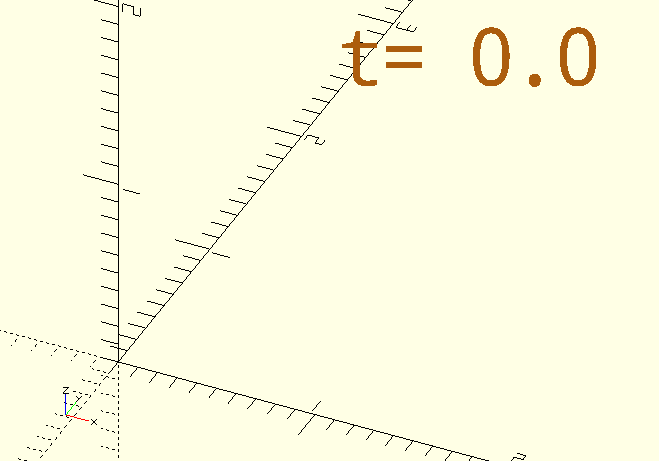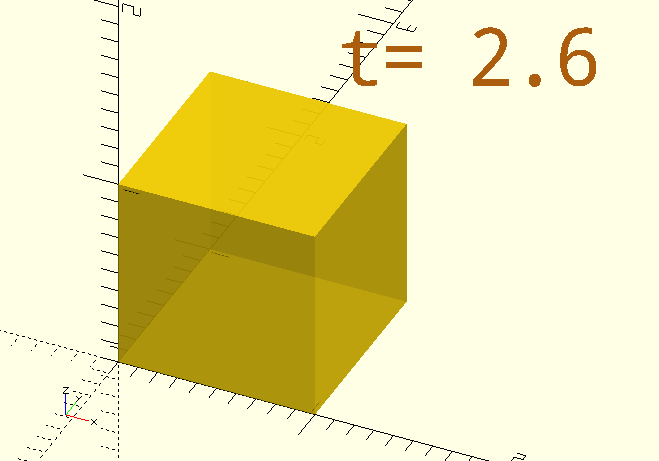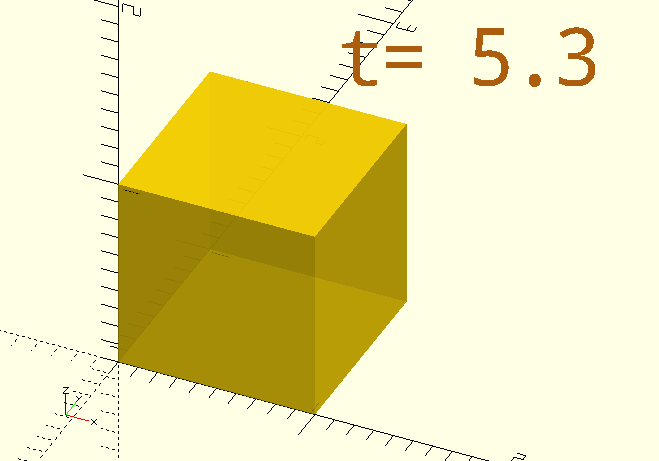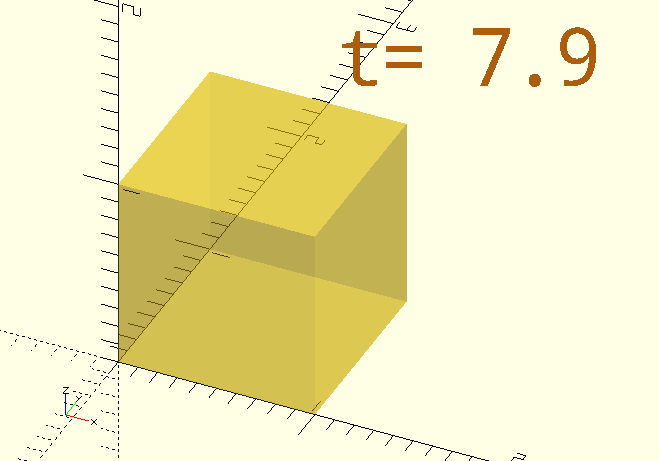
Fraction direct use

Animate() gives quick and easy control, but with it’s pre-set functions, it’s not very adaptable. To get more control, you can call the functions that create the special variables for Animate() directly. You do however still need Animate() to switch the object on and off. Make sure you use the same AnimVector for both Animate() and the function-generator you’re using to prevent unexpected results.

For example a transparent cube that goes solid at 3 and 5 seconds:

$AnimSegs=8;
AVGoldCube=[1,2,6,8];
Animate(AVGoldCube)
color("gold",0.4+0.6*AnimationFXTriangular(AVGoldCube,2))
cube([1,1,1]);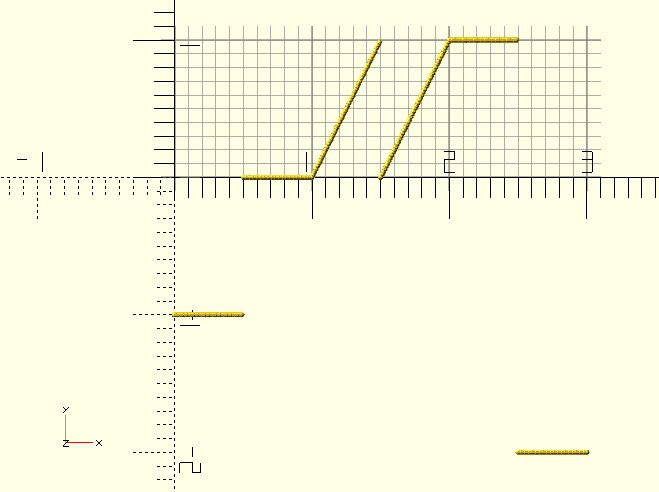

AnimationFxFraction

AnimationFxFraction()

AnimationFxFraction(AnimVector,Frequency)

  • AnimVector, a vector of times, determining the state of children(), see Animate().

  • Frequency, the number of times the signal repeats between the start and end of the object’s animation.

This is the basic animation function. Like $t is the fraction of the entire animation sequence in OpenSCAD, AnimationFxFraction() returns the fraction of the object animation period, which is the period over which the object is animated, even though it may exist longer…​.

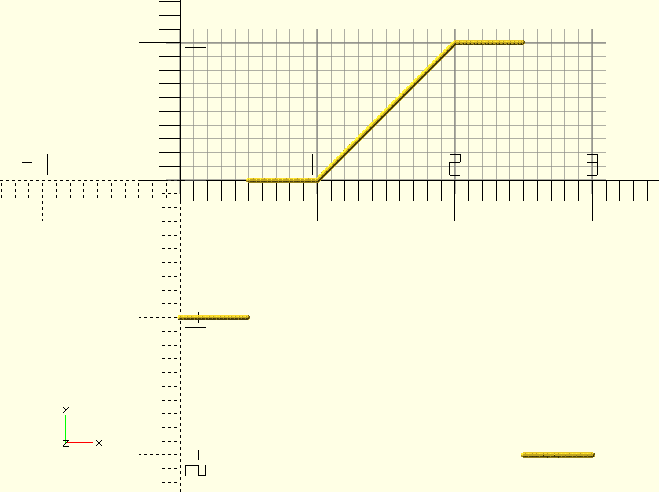
AnimationFxFraction

If an object’s animation period lasts from 1 till 3 seconds, AnimationFxFraction() will be 0.25 at 1.5s, 0.5 at 2s, 0.75 at 2.5s and 1 at 3s, regardless of the length of entire animation sequence. Initial value is -1, switches to 0 at Create, increases linearly to 1 from Start to Finish, stays at 1 until Delete when it drops to -2. The reason for the different pre-Create and post-Delete values of -1 and -2 is to allow for differentiation between the two in the calling routine.
Frequency> 1 creates a saw-tooth-like triangular (wave) signal between Start and Finish.

The first example (above) has a Frequency of 2, and the animation lasts from 1 to 2. This example (right) has a Frequency of 1, which is the default. Notice how in both cases the signal starts at Create at 0.5 seconds, and ends at Delete at 2.5 seconds.

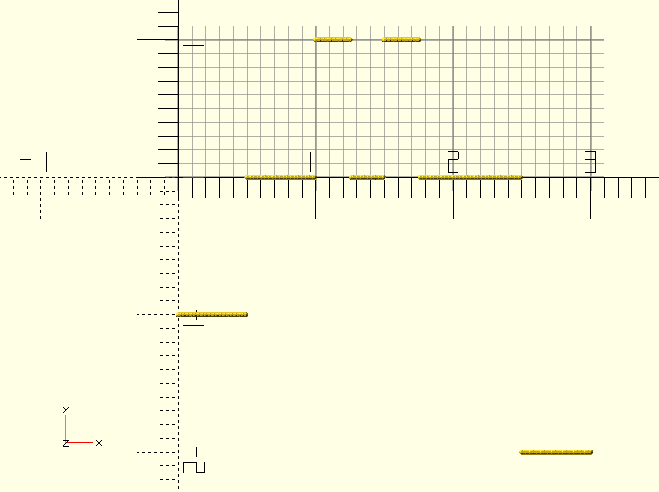
AnimationFxSquare

AnimationFxSquare()

AnimationFxSquare(AnimVector,Frequency)

  • AnimVector, a vector of times, determining the state of children(), see Animate().

  • Frequency, the number of times the signal repeats between the start of the object’s animation and the end.

A 'square wave' signal, or binary flip-flop; switches between 0 and 1 from Start to Finish.

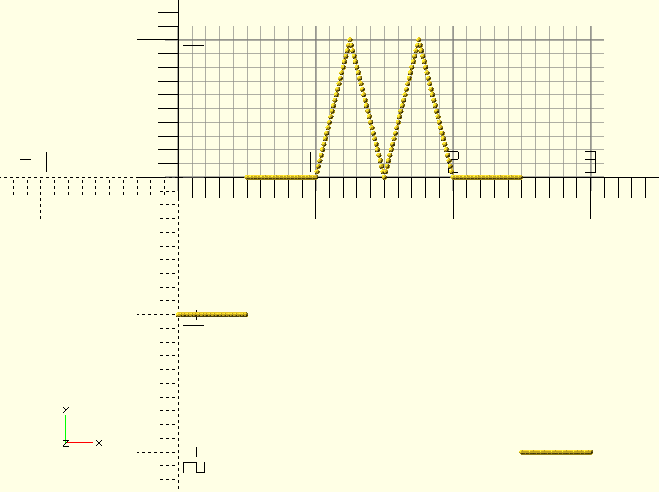
AnimationFxTriangular

AnimationFxTriangular()

AnimationFxTriangular(AnimVector,Frequency)

  • AnimVector, a vector of times, determining the state of children(), Animate().

  • Frequency, the number of times the signal repeats between the start of the object’s animation and the end.

A triangular 'sawtooth' function.

AnimationFxTwoSines()

AnimationFxTwoSines(AnimVector,Base,SinVectorA,SinVectorB,Max)

  • AnimVector, a vector of times, determining the state of children(), see Animate().

  • Base, minumum, 'lift' the function up from the X-axis.

  • SinVector, a vector [Amplitude,Domain,Power] describing the sinusoid function, see description below.

  • Max, clip the function at Y=Max.

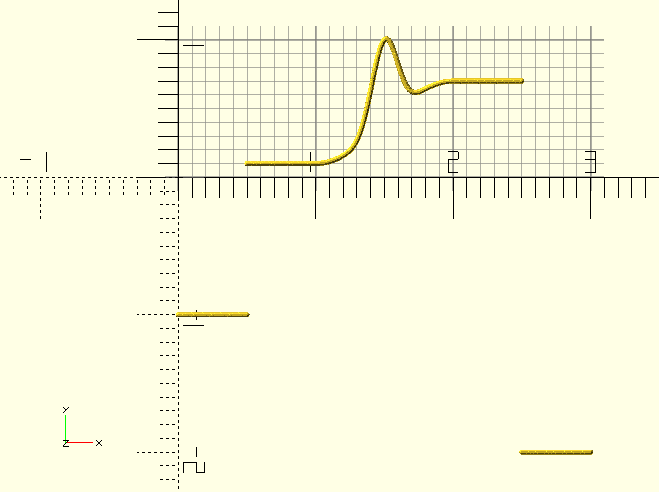
AnimationFxTwoSines

This is the holy grail of animation signal generators. Well, maybe not, but it’s pretty neat anyway. Most of the special animation variables that Animate() generates are made with this signal function. It is highly customisable and has it’s own demo file, it pays off to check that out…​

The function is the sum of two sinusoid functions, each sinusoid function has it’s own SinVector [Amplitude,Domain,Power] defining the curve.

The Amplitude speaks for itself, Domain is expressed in degrees; a domain of 180 means a 180 degree sinusoid will be generated within the length of the animation segment. Because (usually) only 90 or 180 degrees of sinusoid are used—​as this gives the best results—​odd powers can be used the same as even powers; the negative range part of the curve never comes into play.

Higher Power gives narrower 'Bumps' for the 180 degree curve, and bigger delays before the 90 degree curve starts to rise.

The function has a Base-line capability; this lifts the whole function up by the value of Base. The amplitude of the remainder should be reduced to 1-Base to keep the range [0,1]--if so desired.

Using a 180 degree Domain for the second function gives the capability to add a 'Bump' to the curve, this looks good for sphere sizes, overshooting and then returning to their size proper.

TheGHOUL/DemoFiles/AnimationFxDemo.scad, illustrates the use of this and the other functions. Go play around with it.

Tip Or you can just go to the Desmos Graphing Calculator, the link opens in a new tab with the function field already populated, you can dive right in—​pay attention to the domain.
Table 1. A few SinVector examples that work well:
Base SinVectorA SinvectorB Comment

0

[1,90,4]

[1.5,180,6]

Bounce-size for spheres.

0

[1,90,4]

[0.8,180,6]

Bump-size for cylinders.

0.3

[0.7,90,20]

[0,180,2]

Alpha.

0

[0,90,1]

[3,180,6]

With Max=1, for Fade-in Fade-out.

OpenSCAD and CSS.

CSS? Only kidding, but there’s a neat feature in CSS; the cubic-bezier() function. If Bézier curves are alien to you, have a look at—​and play with them—​here: cubic-bezier.com. Go ahead,it’s worth a look, or take a look at the Bézier curve primer right here in The GHOUL’s documentation. TheGHOUL has two functions, similar to the CSS functions, BezierTransitionUp() and BezierTransitionDown(), which can be helpful for quick and simple animations.

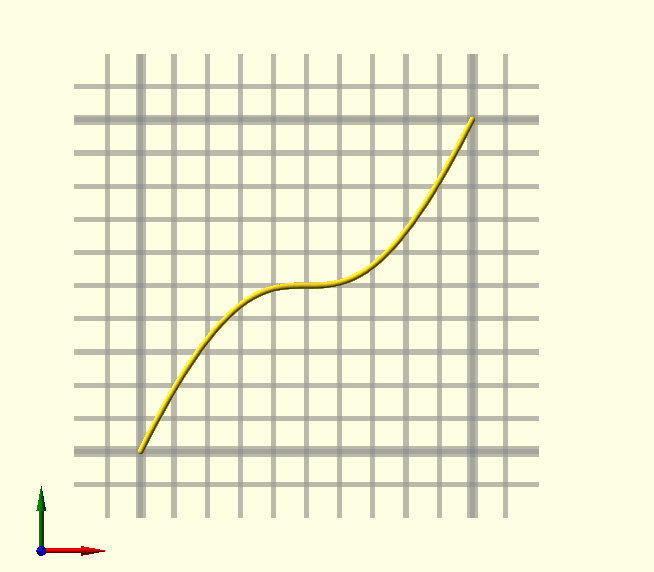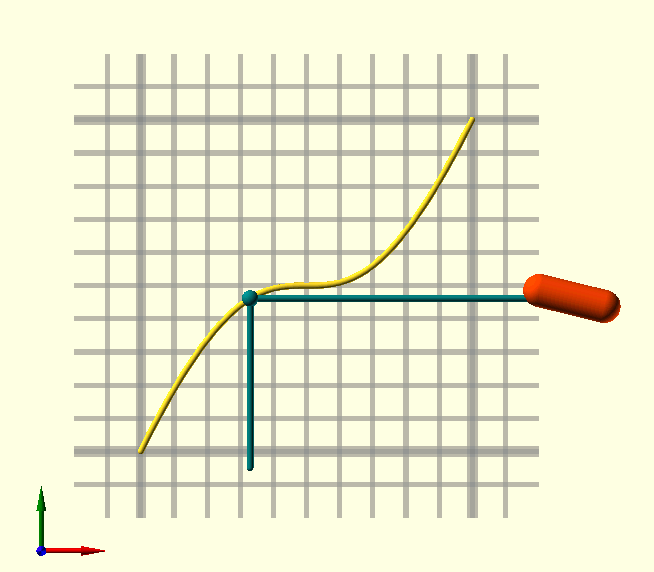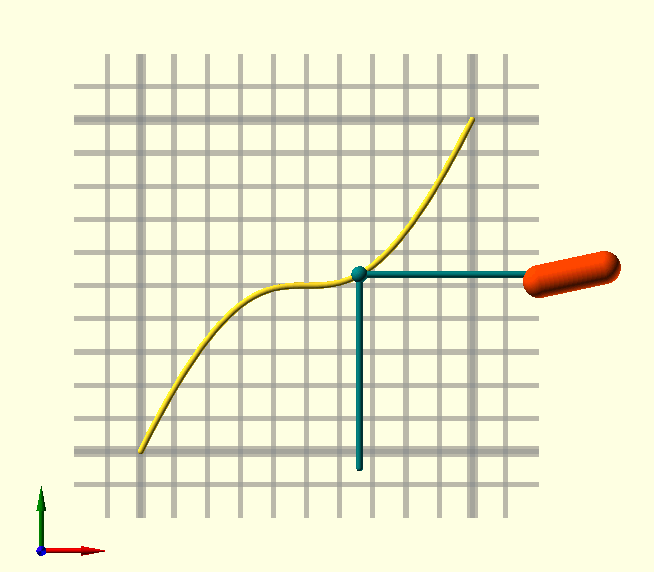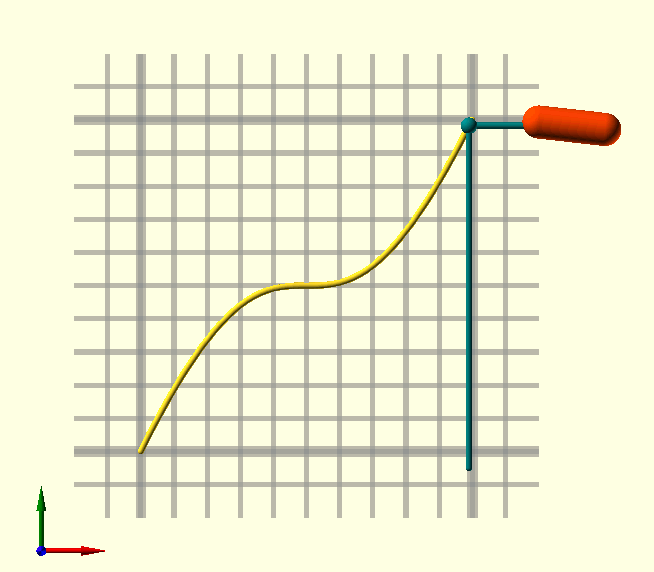
BezierTransitionUp

BezierTransitionUp()

BezierTransitionUp(X1,Y1,X2,Y2,Frac=undef,Res=0.01)

  • X1…​Y2, control point coordinates.

  • Frac, fraction, point on the curve to return, leave undef for animation sequences.

  • Res, fraction, resolution, e.g., 0.01 for 100 steps, defaults to 0.001.

Use BezierTransitionUp() in 'Animate()' sequences, like translation and rotation in the accompanying image. When Frac is left undef, the animation fraction $AnFrac is used, this function is meant for animation sequences after all…​ With BezierTransitionUp() and it’s sibling BezierTransitionDown(), it’s easy to transition smoothly from one state to another in your animation, it can be used for any parameter, in translations, color changes, rotations, whatever takes your fancy.

Animate([0,10]){

    // BezierTransitionUp() uses $AnFrac by default, so no need
    // to specify a fraction value for the transition.
    TRN=BezierTransitionUp(0.5,1,0.5,0);

    color(ORD)
    translate([1.3,TRN,0])
    rotate([0,0,TRN*360])
    BallCylinderBetween([-0.1,0,0],[0.1,0,0],Radius=0.05);

    color(DCN){
        translate([$AnFrac,TRN,0])
        sphere(r=0.025);
        BallCylinderBetween(
            [$AnFrac,-0.05,0],
            [$AnFrac,TRN,0],Radius=0.01);
        BallCylinderBetween(
            [$AnFrac,TRN,0],
            [1.3,TRN,0],Radius=0.01);
    }
}

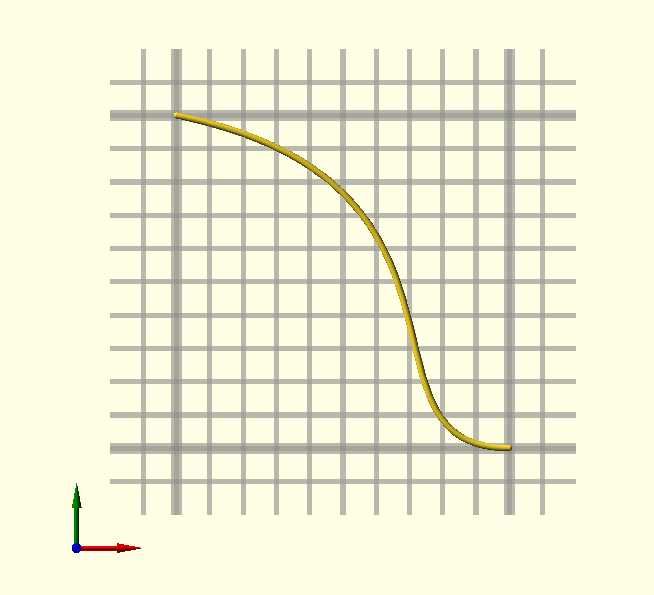
BezierTransitionDown

BezierTransitionDown()

BezierTransitionDown(X1,Y1,X2,Y2,Frac=undef,Res=0.01)

  • X1…​Y2, control point coordinates.

  • Frac, fraction, point on the curve to return, leave undef for animation sequences.

  • Res, fraction, resolution, e.g., 0.01 for 100 steps, defaults to 0.001.

Like BezierTransitionUp(), but down…​