And while I stood there I saw more than I can tell and I understood more than I saw; for I was seeing in a sacred manner the shapes of all things in the spirit, and the shape of all shapes as they must live together like one being.
Lovely, shapely shapes.
Shapes are rotate_extrude() or linear_extrude()-able 2D polygons. Polyhedrons and other 3D primitives as well as explicitly extruded objects can be found on the
Objects page. 'Directional' shapes or such shapes that could be considered to have a directional property have their 'direction' aligned with the positive X-axis. It may pay off to read The GHOUL’s
conventions.
|
Since they are polygon()s, the native offset(){} can be used—like I did with the Star() shape here—to generate new and even more shapely shapes!
|
offset(3){
Star(5,20);
}
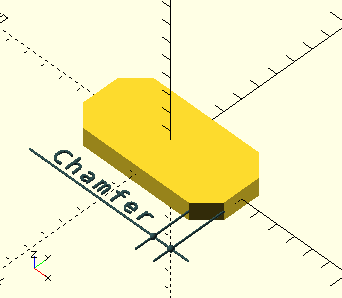
ChamferedRectangle()
A function
ChamferedRectangle(Width,Length,Chamfer,Centered=true)
-
Width, scalar, the X-dimension.
-
Length, scalar, the Y-dimension.
-
Chamfer, scalar, the chamfered corner dimension. The chamfer is measured parallel to one of the sides and not along the chamfered face.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
The ChamferedRectangle.scad file, like all the other Shapes here, provides a function that returns an array; ChamferedRectangle(…)[0] contains the vertices and ChamferedRectangle(…)[1] the face, so you can do:
Shape=ChamferedRectangle(8,4,1);
polygon(Shape[0],Shape[1],2);And a module
However, it makes much more sense to have a module that returns the completed polygon, so you can simply do: ChamferedRectangle(8,4,1); and linear_extrude() it to what you need. Like all the other Shapes here, the file also contains a module that does just that.
Having both the function and the module available gives you the options to do whatever you need with this shape. They both take the exact same call, and OpenSCAD knows which one you are referring to from the call construct:
Var=Shape(...); // clearly refers to the function
translate(...)
linear_extrude(...)
Shape(...); // obviously refers to the moduleOr, you can use just the vertices ChamferedRectangle(8,4,1)[0] and
AffineTransform() them or use them as a profile in a more complex polyhedron.
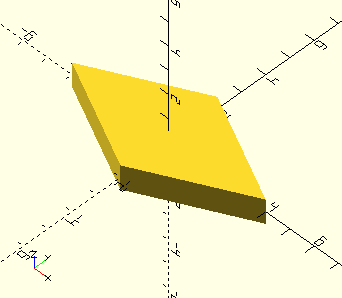
Diamond()
Diamond(Width,Length,Centered=true)
-
Width, scalar, the X-dimension.
-
Length, scalar, the Y-dimension.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Like the other shapes here, there is both a Diamond() function and a module. The function returns an array of vertices Diamond()[0] and a face Diamond()[1] for post-processing or polyhedron generation. The module generates the polygon.
Ellipse()
Ellipse(Radius1,Radius2,Centered=true)
-
Radius1, scalar, radius of the ellipse along the X-axis.
-
Radius2, scalar, radius of the ellipse along the Y-axis.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Like the other shapes here, there is both a Ellipse() function and a module. The function returns an array of vertices Ellipse()[0] and a face Ellipse()[1] for post-processing or polyhedron generation. The module generates the polygon.
|
|
In The GHOUL the
convention is to place 2D shapes and objects with a directional character such as arrows or triangles so they point along the positive X-axis. 3D objects that have a discernable 'top' as well as a directional aspect or 'front', will have the front aligned with the positive X-axis and the top with the positive Z-axis. Maintaining this convention provides predictable results from the Position() and Align() functions and other rotations.
|
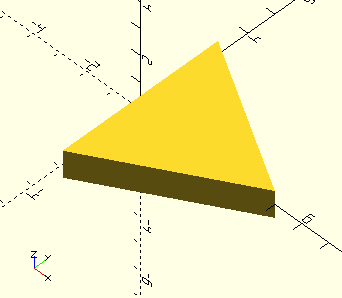
EquilateralTriangle()
EquilateralTriangle(Size,Type="Height",Centered=true)
-
Size, scalar, main dimension, depends on Type.
-
Type, string:
-
Side, the triangle sides will have dimension Size.
-
Height, the triangle apex will be dimension Size above it’s base.
-
Radius, the triangle’s points will be dimension Size from it’s center.
-
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Like the other shapes here, there is both an EquilateralTriangle() function and a module. The function returns an array of vertices EquilateralTriangle()[0] and a face EquilateralTriangle()[1] for post-processing or polyhedron generation. The module generates the polygon.
The Type=Radius version is in essence identical to circle(r=Size,$fn=3), but places the triangle’s apex on the X-axis with it’s base against the Y-axis if Centered=false.
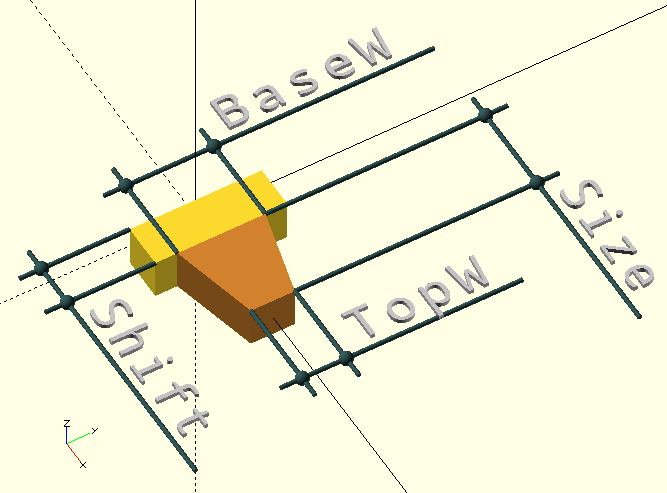
Grooved()
Grooved(Size,BaseW,TopW,Shift=[0,0],Reps=1,Centered=true)
-
Size, scalar, depth of the groove, or height of the tooth…
-
BaseW, scalar, width of the tooth at the base.
-
TopW, scalar, width of the tooth at the top.
-
Shift, 2D vector, translate the tooth in +X and Y units. As the tooth moves away from the Y-axis, the gap is filled with a supporting base for the tooth.
-
Reps, integer, number of teeth or grooves.
-
Centered, Boolean, the shape is centered on the positive X-axis if true, it is placed in the first quadrant if false. Default=true.
Grooved() is intended to be used for the generation of grooved surfaces, for example to enhance grip or reduce reflection. With the right BaseW and TopW it can also generate a 'dovetail' for joining parts, like in the image to the right.
For the curious: Yes, GHOUL has a
Dimension() module to dimension objects, it’s nothing fancy and no threat to Autocad®[1] but it’s very useful for making illustrations like the one above.
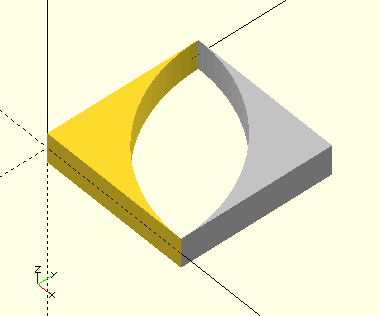
InsideRadius()
InsideRadius(Radius,Centered=true)
-
Radius, scalar, radius…
-
Centered, Boolean, the rotation center of Radius lies on the origin if Centered=true; the silver shape in the image. If Centered=false, the rotation center of Radius lies on [Radius,Radius]; the golden shape in the image. In either case, the shape lies in the first quadrant.
NGon()
NGon(Sides=5,Radius=3,Centered=true);
-
Sides, scalar, number of sides of the polygon.
-
Radius, radial distance of the polygon corners to its center.
-
Centered, Boolean, the shape is centered on the positive X-axis if true, it is placed in the first quadrant if false. Default=true.
Generate a regular polygon. Yes, this is the same as circle(r=…,$fn=…) but with better control over placement when Centered=false, and the added bonus of automatic 'offset' calculation:
|
|
An even-sided regular polygon has its largest dimension of 2*Radius through the corners, its lateral dimension depends on the number of sides. An odd-sided regular polygon has lateral and vertical dimensions that both depend on the number of sides. |
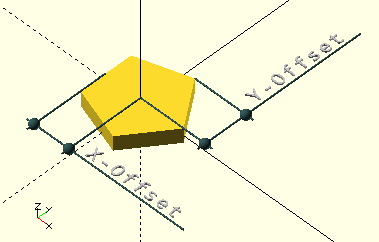
NGon() echos offset values like so: "NGon Offset is [2.42705, 2.85317]", they are dimensions from the radial center; the first value is the absolute of the negative X-dimension; to the flat of odd-sided polygons, to the corner of even-sided polygons, i.e., for the latter it is the same as Radius.
The second value is the Y-dimension; for odd-sided polygons this is to a corner but not radially, for even-sided polygons this is the dimension to a flat side.
The radial dimension from the center to any of the corners is—obviously—the same as Radius.
translate()-ing an NGon() by it’s offset would place it in the first quadrant, touching the axes.
The largest dimension of both odd- and even-sided polygons lies on the positive X-axis, pointing 'East' in accordance with the GHOUL conventions.
To help with manipulation of polygons, NGon.scad contains a helper function that provides the same offset values as the echo in NGon() itself:
NGonOffset(Sides,Radius)
NewVar=NGonOffset(5,3);
echo(NewVar);
ECHO: [2.42705, 2.85317]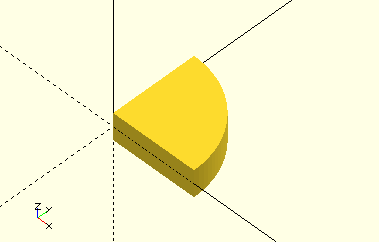
OutsideRadius()
OutsideRadius(Radius)
-
Radius, scalar, radius…
OutsideRadius() generates a 90 degree circle segment in the first quadrant which can be used to generate fillet radii.
OvalRing()
OvalRing(Radius1,Radius2,Wall,Centered=true)
-
Radius1, scalar, radius of the oval ring along the X-axis.
-
Radius2, scalar, radius of the oval ring along the Y-axis.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Like the other shapes here, there is both an OvalRing() function and a module. The function returns an array of vertices OvalRing()[0] and a face OvalRing()[1] for post-processing or polyhedron generation. The module generates the polygon.
PathsToPolygon()
PathsToPolygon(Paths)
-
Paths, an array of arrays of 2D vertices.
PathsToPolygon() turns a number of vertex lists, each forming a polygon, into an OpenSCAD complex (multiple path) polygon notation like [[Points],[Paths]]. I haven’t had reason to write the opposite PolygonToPaths(), but the placeholder is there, and who knows, one day…
Of course, as is The GHOUL’s custom, there is a PathsToPolygon() module as well…
PathsToPolygon([Circle(10,$fn=10)[0],Star(5,4,Schlaefli=2,Centered=false)[0]]);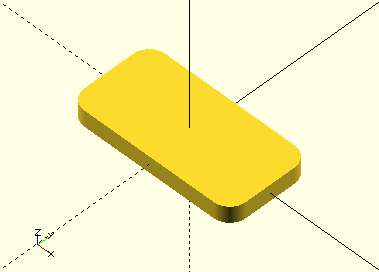
RadiusedRectangle()
RadiusedRectangle(Width,Length,Radius,Centered=true)
-
Width, scalar, the X-dimension.
-
Length, scalar, the Y-dimension.
-
Radius, scalar, the corner radii.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Both a RadiusedRectangle() function and a module are provided. The function returns an array of vertices RadiusedRectangle()[0] and a face RadiusedRectangle()[1] for post-processing or polyhedron generation. The module generates the polygon.
RectangularProfile()
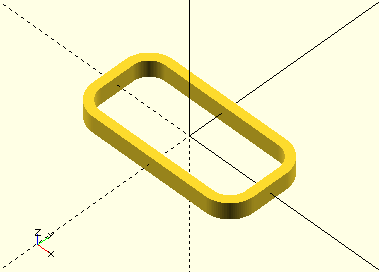
RectangularProfile(Width,Length,Wall,Radius,Centered=true)
-
Width, scalar, the X-dimension.
-
Length, scalar, the Y-dimension.
-
Wall, scalar, the wall thickness.
-
Radius, scalar, the corner radii.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Both a RectangularProfile() function and a module are provided. The function returns an array of vertices RectangularProfile()[0] and a face RectangularProfile()[1] for post-processing or polyhedron generation. The module generates the polygon.
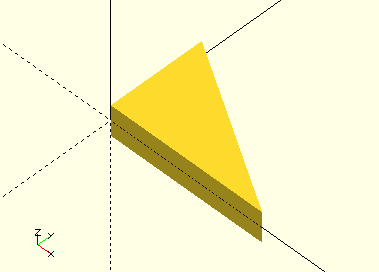
RightTriangle()
RightTriangle(Width,Length)
-
Width, scalar, the X-dimension.
-
Length, scalar, the Y-dimension.
A bit trivial , this one…
Ring()
Ring(Radius,Wall,Centered=true)
-
Radius, scalar, radius of the ring.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Like the other shapes here, there is both a Ring() function and a module. The function returns an array of vertices Ring()[0] and a face Ring()[1] for post-processing or polyhedron generation. The module generates the polygon.
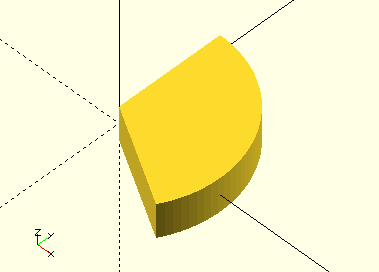
Sector()
Sector(Start,End,Radius)
-
Start, angle, start of the sector. Angles are expressed CCW from the positive X-axis.
-
End, angle, end of the sector. Angles are expressed CCW from the positive X-axis.
-
Radius, scalar, radius of the sector.
Like the other shapes here, there is both a Sector() function and a module. The function returns an array of vertices Sector()[0] and a face Sector()[1] for post-processing or polyhedron generation. The module generates the polygon.
Sector() is very useful in difference() or intersection() operations for cutting sectors out of any of the circular shapes or OpenSCAD primitives.
To make this a little easier,
SectorSlice() from the
Modifiers library accepts Height, Centered and Convexity parameters and performs an intersection() operation on it’s children().
SectorCut() does the same, but with a difference() operation, it removes a sector from its children().
The correct convexity parameter is important, especially when using difference() operations for example on objects that have been linear_extrude()-ed or SectorCut(). When convexity settings are too low, ugly 'artifacts' may appear that spoil your preview.
As per the OpenSCAD manual: "The convexity parameter specifies the maximum number of front sides (back sides) a ray intersecting the object might penetrate. This parameter is only needed for correctly displaying the object in OpenCSG preview mode and has no effect on the final rendering."
Also see the OpenSCAD
FAQ entry
on this subject, as well as the OpenSCAD
manual entry.
Square()
Square(Width,Length,Centered=true)
-
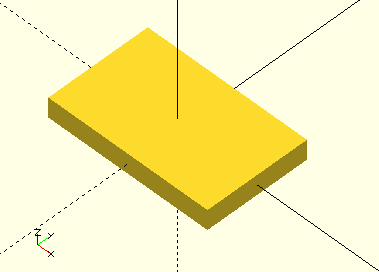
Width, scalar, the X-dimension.
-
Length, scalar, the Y-dimension.
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Yes, OpenSCAD has a perfectly good square() module, but there’s more to Square.scad: The file provides a function that returns an array; Square()[0] contains the vertices and Square()[1] the face. These arrays can be post-processed, used as profiles in polyhedrons &c. and that is the real reason for it’s existence. It also contains a module that returns the completed polygon. The module is indeed a bit superfluous…
Star()
Star(Points,Radius,Schlaefli=2,Centered=true);
-
Points, scalar, number of points of the star polygon.
-
Radius, radial distance of the star’s points to its center.
-
Schlaefli, number,
-
When given as a fraction (0…1)[2] it is the ratio between internal and external point radii, this is unlikely to result in a regular star polygon. Probably.
-
When given as an integer [1,2,…) it is the Schläfli turning number. A Schäfli turning number can be interpreted as "connect the current point with a straight line to the current point plus Schläfli number". A Schläfli number of 1 yields a regular polygon, each point connected to the next, and the polygon is drawn in 1 'turn'. A Schläfli number of 2 yields the first possible regular star polygon, each point connected to the one after the next, and the polygon is drawn in 2 'turns'. The Schläfli number must be an integer less than Points/2. A Schläfli number of approximately
floor(Points/3)yields the 'prettiest' stars[3]. Also see Wikipedia.
-
-
Centered, Boolean, the shape is centered on the origin if true, it is placed in the first quadrant if false. Default=true.
Generate a regular star polygon shape. Regular star polygons have at least 5 points. Star() is closely related to NGon().
An even-pointed regular star polygon has its largest dimension of 2*Radius through the points, its lateral dimension depends on the number of points. An odd-pointed regular star polygon has lateral and vertical dimensions that both depend on the number of points.
Star() echos offset values like so: "Star Offset is [2.42705, 2.85317]", they are dimensions from the radial center; the first value is the dimension to the 'base points' of odd-pointed polygons, for even-pointed polygons it is Radius. The second value is the extreme Y-dimension; for both odd and even pointed polygons this is the floor(Points/4)-th point. The dimension from the center to the point on the positive X-axis is always Radius.
The largest dimension of both odd- and even-pointed polygons lies on the positive X-axis, pointing 'East' in accordance with the GHOUL conventions.
To help with manipulation of polygons, Star.scad contains a helper function that provides the same offset values as the echo in Star() itself:
StarOffset(Sides,Radius)
NewVar=StarOffset(5,3);
echo(NewVar);
ECHO: [2.42705, 2.85317]