I am not Victor any more. Victor was my nerd name; now I’m Vector!
— Victor Perkins

Things can get murky, but according to Wikipedia , "In mathematics and physics, a vector is an element of a vector space." That works for me. In The GHOUL, I’m using vector for a tuple of no more than 3, sometimes homogenised to 4, elements, representing a 2D or 3D vertex or vector.

The routines.

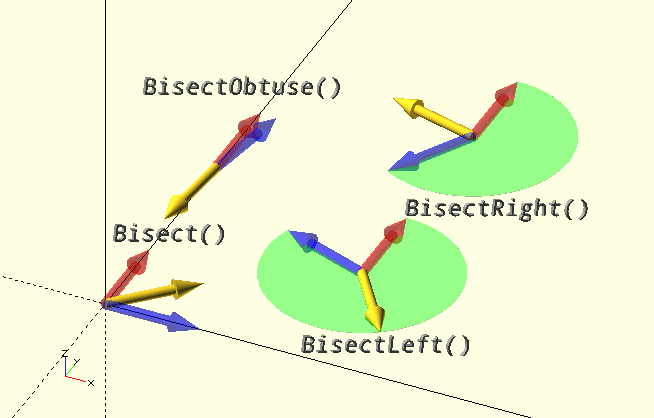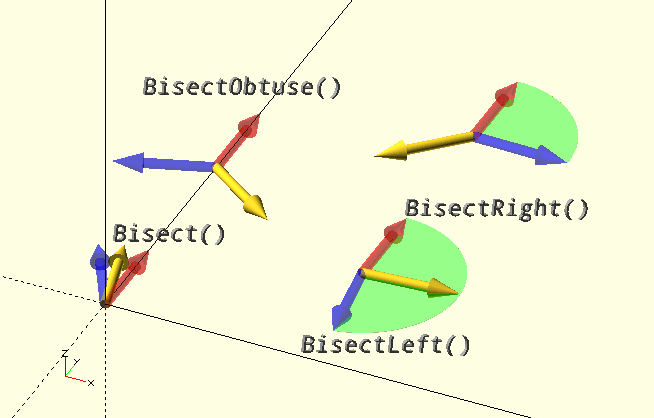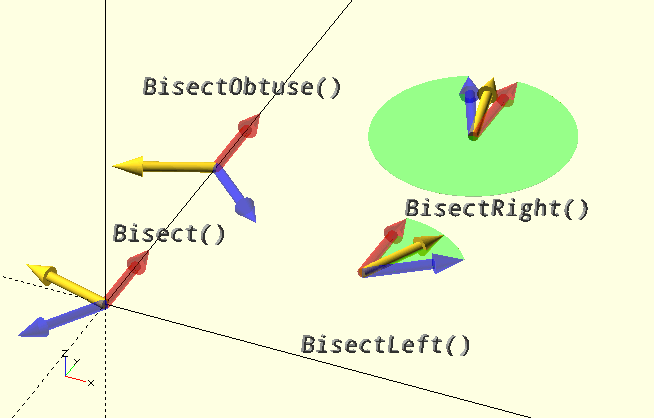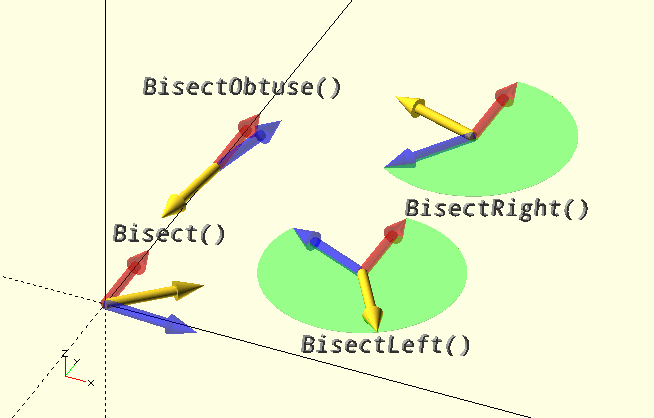
Bisect

Bisect()

Bisect(V1,V2,V3)

  • V1, V2, V3, vertices or vectors, 2D or 3D.

Bisect() Returns a unit vector with the direction of the line that bisects the acute angle between two vectors, or the two line segments starting at V2 and ending in V1 and V3, in the plane defined by the two vectors or line segments.

If three parameters are are specified, they are treated as vertices and the unit vector bisecting the acute angle of the line segments V2-V1 and V2-V3 is returned. If only two parameters are specified, they are treated as vectors and the unit vector bisecting their acute angle is returned.

In the limit case where the line segments or vectors are collinear and unlike (opposing), the LPerpVector() of the second vector V2 or of line segment V2-V3 will be returned.

In the limit case where the line segments or vectors are collinear and like (having the same direction), the unit vector of the the first vector V1 or of line segment V2-V1 will be returned.

Important Although Bisect() and its cousins (below) will accept 3D vectors and vertices, they were made for the 2D scenario. In 3D, when two vectors are on the same line (concurrent and collinear), they do not define a plane, and thus there is not one perpendicular line, but only a perpendicular plane. In this case, the vector perpendicular to the projections of the two vectors on Z=0, in accordance with the above caveats for the limit cases will be returned, effectively ignoring any 3D aspect. 
echo([Bisect([2,6],[7,-3])]);

ECHO: [0.91224, 0.409656]

Bisect() has three cousins that have slightly different behaviour:

BisectObtuse()

Does the exact reverse of what Bisect() does, it bisects the obtuse angle of the vectors or line segments. It is an alias for -Bisect().

In the limit case where the the line segments or vectors are collinear and unlike, it returns the RPerpVector() of the second vector V2 or of line segment V2-V3.

In the limit case where the the line segments or vectors are collinear and like, the unit vector opposing the vectors or line segments will be returned.

BisectLeft()

Always bisects to the left, i.e. in a counter-clockwise direction from the second vector, or line segment V2-V3. If the vertices are successive vertices of a polygon boundary, in CCW order, the bisector will always point into the polygon. This is used by Offset() to create offset boundaries or lines. (The polygon area is indicated by the green sectors in the image above.)

In the limit case where the line segments or vectors are collinear and unlike, the LPerpVector() of the second vector V2 or of line segment V2-V3 will be returned, as it is by Bisect().

In the limit case where the line segments or vectors are collinear and like, the unit vector of the vectors or line segments will be returned, as it is by Bisect().

BisectRight()

Always bisects to the right, i.e. in a counter-clockwise direction from the second vector, or line segment V2-V3. If the vertices are successive vertices of a polygon boundary, in CCW order, the bisector will always point out of the polygon. This is used by Offset() to create offset boundaries or lines.

In the limit case where the vertices or vectors are colinear and unlike, the RPerpVector() of the second vector V2 or of line segment V2-V3 will be returned, as it is by BisectObtuse().

In the limit case where the vertices or vectors are collinear and like, the unit vector opposing the vectors or line segments will be returned, as it is by BisectObtuse().

CrossProduct()

CrossProduct(Vector1,Vector2))

  • Vector1 and Vector2, vectors with the same dimensionality, i.e., 2D or 3D &c.

Returns the cross product of two vectors. The native function cross() only accepts vectors of length 3, which is fine, so this is a bit superfluous. Probably. Unless you want the cross product of a 4D vector…​

Vector=CrossProduct([1, 2, 3, 4], [5, 6, 7, 8]);
echo(Vector);

ECHO: [-4, -4, 12, -4]

DotProduct()

DotProduct(Vector1,Vector2)

  • Vector1 and Vector2, vectors with the same number of coordinates.

Returns the dot product of two vectors. A bit silly really because you can just do Vector1*Vector2, so this is a bit superfluous. Really. But maybe it makes for clearer code.

Vector=DotProduct([1, 2, 3], [4, 5, 6]);
echo(Vector);

ECHO: 32

HomogeniseVector()

HomogeniseVector(Vector)

  • Vector, a 2D or 3D vector.

Returns the homogenous coordinates form of Vector. If Vector is 2D, it will be promoted to 3D first.
Used for affine transformation.

Vector=HomogeniseVector([1, 2]);
echo(Vector);

ECHO: [1, 2, 0, 1]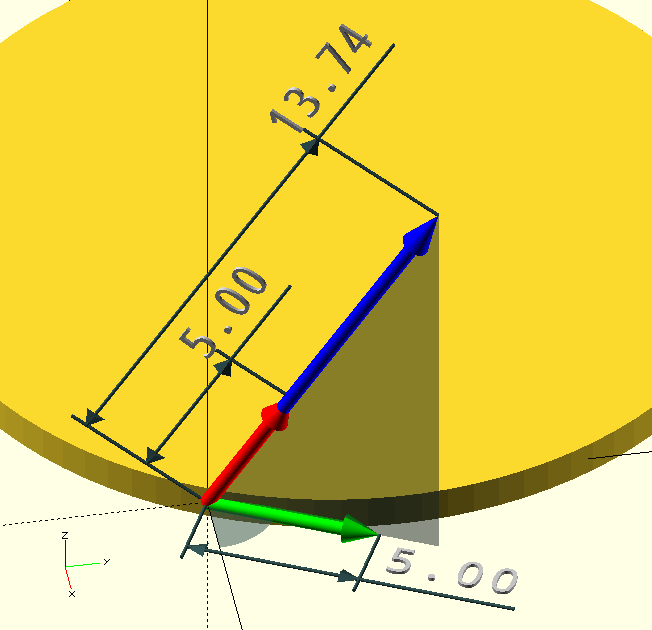

LengthVector

LengthVector()

LengthVector(VectorOrAngle,Length)

  • VectorOrAngle, either a 3D vector, or Azimuth angle.

  • Length, scalar, length of the returned vector.

Returns a vector of the requested length. When called with a vector, the returned vector will be colinear with, and like the input vector, but of length Length (the red one in the image). When called with an angle, the returned vector is of length Length, in the direction of the angle and in the plane Z=0 (the green one in the image).
I don’t remember why I thought the circular slab made a good background for the examples in the image…​

Foo=[3,6,12];
Bar=LengthVector(Foo,5);
Baz=VectorToIncAz(Foo).z;
echo(Baz);                  // ECHO: 63.4349
Boz=LengthVector(Baz,5);

color(BLU)
Arrow(Foo,Base=[0,0,0],Points=[0,2],Thickness=0.4);
color(RED)
Arrow(Bar,Base=[0,0,0],Points=[0,2],Thickness=0.42);
color(GRN)
Arrow(Boz,Base=[0,0,0],Points=[0,2],Thickness=0.42);

LPerpVector()

LPerpVector(Vector,Length)

  • Vector, a vector in 2D, if Vector is 3D, it is first 'projected' onto the X-Y plane, that is to say, Vector.z is forced to 0.

  • Length, length of the returned vector.

Returns a vector 90 degrees left (perpendicular) to Vector. This can be used to create an offset path from a 2D Shape, although Offset() would be better for that.

Vector=LPerpVector([1, 1],4);
echo(Vector);

ECHO: [-2.82843, 2.82843]

Modulus()

Modulus(Vector)

  • Vector, a vector, probably 3D or 2D.

Returns the magnitude or length a.k.a. 'modulus' of a vector. This is the same as the native OpenSCAD function norm(). Yep. But I’m used to calling it 'modulus of a vector', so it’s here just to please myself, as is this entire project, really.

Vector=Modulus([1,2,3]);
echo(Vector);

ECHO: 3.74166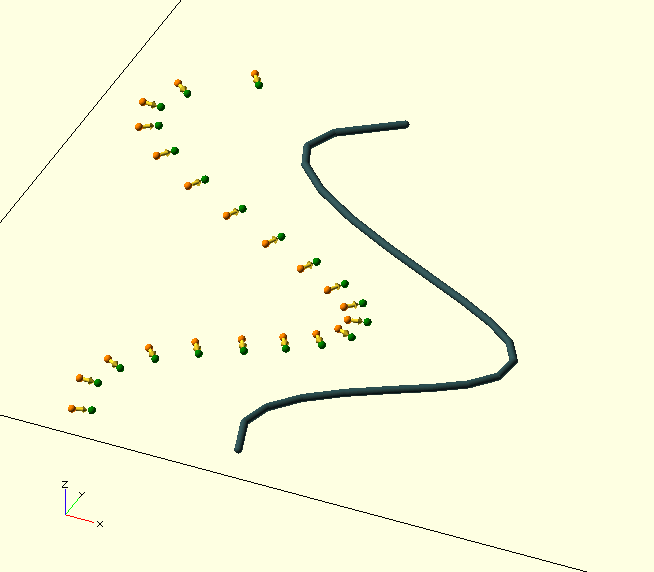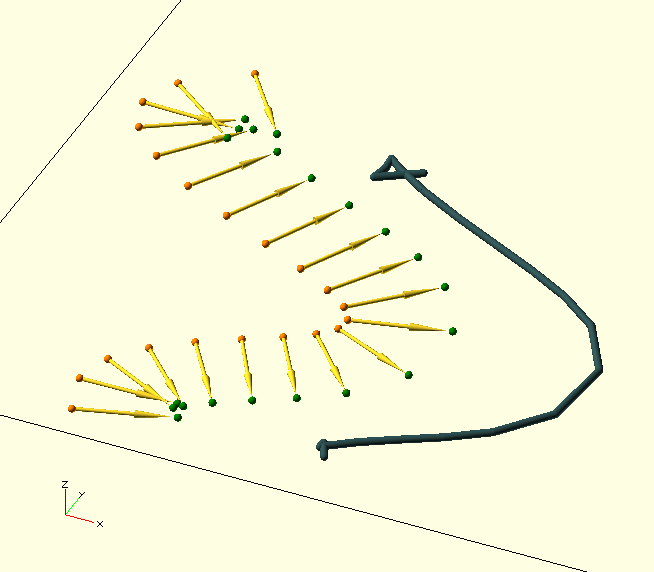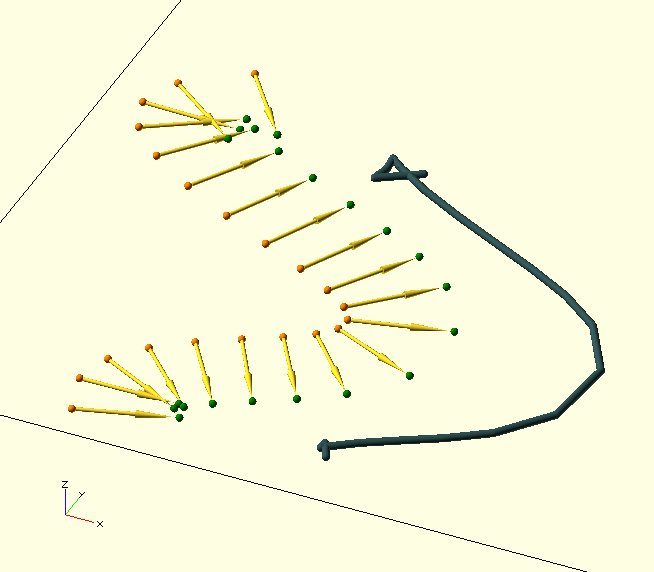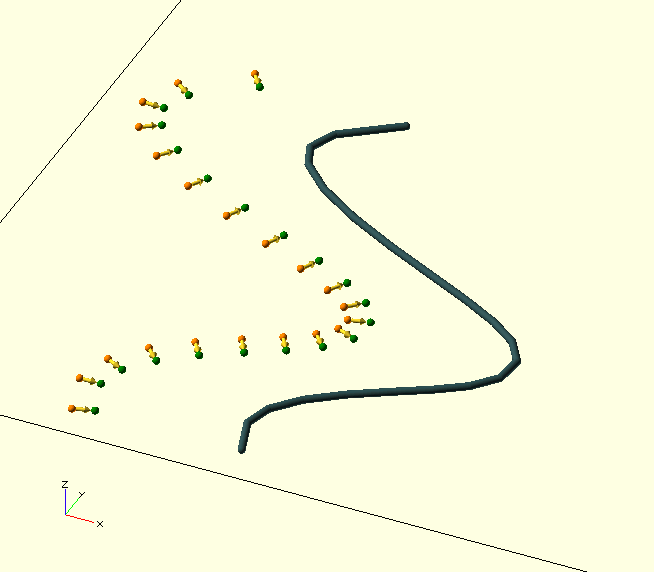

OffsetCurve

Offset()

Offset(V1,V2,V3,Dist)

  • V1, V2, V3, vertices, 2D or 3D.

  • Dist, scalar, distance to offset the vertex.

Offset() and it’s relations are simply Bisect() with the distinction that the bisecting vector will be given length Dist and added to vertex V2, i.e., V2 is offset by Dist in the direction of the requested bisector.

OffsetLeft() and OffsetRight() are the only ones that have a use (unless I’ve overlooked/not yet realised something). OffsetAcute() and OffsetObtuse() only exist in the name of completeness, because their Bisect() cousins do. Offset() is an alias for OffsetAcute(). For more information on Offset() and it’s kin, check out the Bisect() family of functions.

Note OffsetLeft() and OffsetRight() were written specifically for the manipulation of polygon boundaries, but caution is warranted: Where the offset direction is such that it reduces the radius of curvature, and the offset value is chosen larger than this original, local curvature of the curve, the curve will be deformed and fold back across itself, effectively invalidating the polygon boundary as such. (Like wot’s goin' on in the GIF.)

PolarToVector()

PolarToVector(Polar,Force3D=false)

  • Polar, polar coordinates, physics convention, i.e., [Radius, Inclination, Azimuth] or [Radius, Azimuth] where:

    • Radius, Length of the resulting vector.

    • Inclination, Angle from the positive Z-Axis in degrees (0-180 inc.).

    • Azimuth, Angle CCW from the positive X-axis in degrees (0-360).

  • Force3D, Boolean, force 3D coordinates, even with 2D input (appends 0 Z-coordinate).

Convert 'polar' or 'spherical' coordinates to vector coordinates.

ProjectVector()

ProjectVector(Vector)

  • Vector, a homogenised vector.

Projects the homogenised Vector back onto cartesian coordinates. Used after an affine transformation.

Vector=ProjectVector([1,2,3,0.1]);
echo(Vector);

ECHO: [10, 20, 30]

RPerpVector()

RPerpVector(Vector,Length)

  • Vector, a vector in 2D, if Vector is 3D, it is first 'projected' onto the X-Y plane, that is to say, Vector.z is forced to 0.

  • Length, length of the returned vector.

Like LPerpVector(), but to the right…​ Returns a vector 90 degrees right (perpendicular) to Vector. This can be used to create an offset path from a 2D shape, although Offset() would be better for that.

Vector=RPerpVector([1, 1],4);
echo(Vector);

ECHO: [2.82843, -2.82843]

SegmentDirection()

SegmentDirection(Vertex1,Vertex2)

  • Vertex1, Vertex2, 2D or 3D vertices.

Used to find the 'tangent' to a curve, i.e. the direction of a curve segment. To find the tangent at a vertex, try using the vertices either side of the vertex of interest for a (possibly) neater result. Returns the direction in an Inclination and Azimuth tuple [0,Inc,Az]. Uses VectorToIncAz(), also see there.

StartDirection()

StartDirection(VertexList)

  • VertexList, array of 2D or 3D vertices.

Used to find the starting direction of a curve, i.e. the direction of the first curve segment. Returns the direction in an Inclination and Azimuth tuple [0,Inc,Az].

EndDirection()

EndDirection(VertexList)

  • VertexList, array of 2D or 3D vertices.

Used to find the ending direction of a curve, i.e. the direction of the last curve segment. Returns the direction in an Inclination and Azimuth tuple [0,Inc,Az].

UnitVector()

UnitVector(Vector)

  • Vector, a vector.

Returns the unit vector of Vector

Vector=UnitVector([1, 2, 3]);
echo(Vector);

ECHO: [0.267261, 0.534522, 0.801784]

VectorAngle()

VectorAngle(Vector1,Vector2)

  • Vector1 and Vector2, vectors of the same dimensionality.

Returns the angle between the two vectors.

Vector=VectorAngle([1,1,0], [0,1,1]);
echo(Vector);

ECHO: 60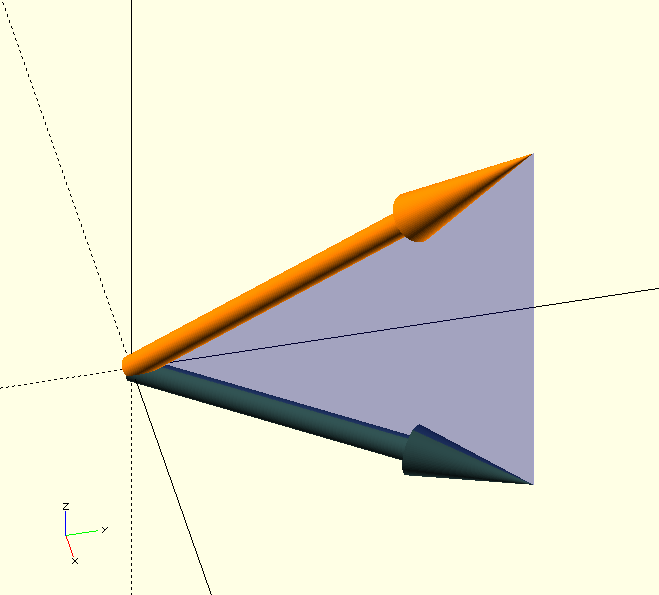

VectorProject

VectorProject()

VectorProject(Vector,Dim=2)

  • Vector, a vector.

  • Dim, index, coordinate to force to 0, defaults to 2.

VectorProject() forces the Dim coordinate of Vector to 0. Dim defaults to 2, so the default behaviour is to return the projection of a 3D Vector onto Z=0.

color(DOG)
Arrow([3,4,5],Points=[0,0.3,1],Thickness=0.3,Base=[0,0,0]);
color(DSG)
Arrow(VectorProject([3,4,5]),Points=[0,0.3,1],Thickness=0.3,Base=[0,0,0]);

color(BLU,0.2)
rotate([90,0,atan(4/3)])
translate([0,0,-0.005])
linear_extrude(0.01)
polygon([[0,0],[5,0],[5,5]]);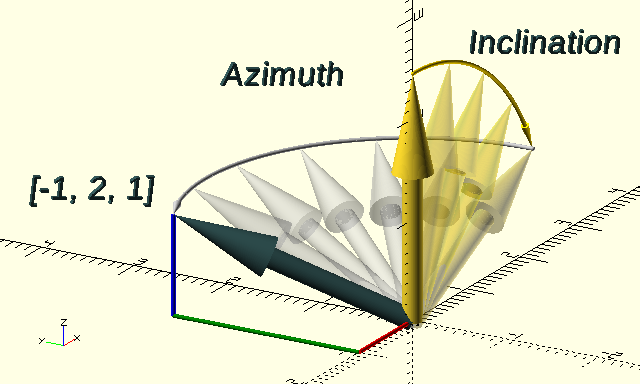

IncAzToVector

VectorToIncAz()

VectorToIncAz(Vector)

  • Vector, a 2D or a 3D vector.

Convert Vector to Azimuth and Inclination angles, as used in polar coordinates, expressed as a tuple, in fact, VectorToIncAz() is VectorToPolar() but with Radius=0 in the result.
The resulting tuple can be used for the native OpenSCAD rotate() function to align an object with Vector. The object must be aligned with the positive Z-axis before the rotation, or in other words, whatever is pointing straight up in the positive Z-direction will be pointing the same way as the Vector after the rotate().
If Vector is 2D, a 0 Z-coordinate will be appended for compatibility.

Vector=VectorToIncAz([-1,2,1]);
echo(Vector);

ECHO: [0, 65.9052, 116.565]

VectorToPolar()

VectorToPolar(Vector)

  • Vector, a 2D or a 3D vector.

Convert Vector to polar coordinates, expressed as a tuple containing [Radius,Inclination,Azimuth].

PolarCoords=VectorToPolar([-1,2,1]);
echo(PolarCoords);

ECHO: [2.44949, 65.9052, 116.565]