Unfortunately, no one can be told what The Matrix is.
— Morpheus
The matrix

Matrices are transformation magic. They allow us to move, skew, rotate and whatever else, entire arrays of vertices, a finished mesh, or a single point. They are versatile and with a little study, pretty easy to work with. The GHOUL makes it all a bit easier with predefined routines for all kinds of transformations.

According to Wolfram-Mathworld:

An affine transformation is any transformation that preserves collinearity (i.e., all points lying on a line initially still lie on a line after transformation) and ratios of distances (e.g., the midpoint of a line segment remains the midpoint after transformation). In this sense, affine indicates a special class of projective transformations that do not move any objects from the affine space ℝ3 to the plane at infinity or conversely. An affine transformation is also called an affinity.

Tip If you’d like some more background, here are a few primers: Affine transformation on this Wikipedia page and here’s another decent primer on neutrium.net, and some more on matrices on Wikipedia.

Affine transformation uses homogenised coordinates, if you’re interesed, here is some good information:

From Wikipedia: Homogeneous coordinates have a range of applications, including computer graphics and 3D computer vision, where they allow affine transformations and, in general, projective transformations to be easily represented by a matrix.

And a bit later in the same article: Homogeneous coordinates are ubiquitous in computer graphics because they allow common vector operations such as translation, rotation, scaling and perspective projection to be represented as a matrix by which the vector is multiplied. By the chain rule, any sequence of such operations can be multiplied out into a single matrix, allowing simple and efficient processing.

Note The examples given below are trivial because they could easily have been accomplished with native OpenSCAD transformations, however, they are examples, normally these transformation matrices would be used to manipulate vertices and arrays before they become objects.

Affine transformers

AffineRotate()

AffineRotate(Vector,List,Angle=undef,Output2D=false)

  • Vector, an openSCAD rotate() vector [x,y,z], or—​when Angle is specified—​a rotation axis.

  • List, an array of vertices or a single vertex.

  • Angle, rotation angle with Vector as axis.

  • Output2D, force 2D output, even with 3D input, i.e., crop the Z-coordinate.

Perform affine transformation on an array of vertices. Returns 3D or 2D consistent with input.

AffineScale()

AffineScale(Vector,List,Output2D=false)

  • Vector, an openSCAD scale() vector [x,y,z].

  • List, an array of vertices or a single vertex.

  • Output2D, force 2D output, even with 3D input, i.e., crop the Z-coordinate.

Perform affine transformation on an array of vertices. Returns 3D or 2D consistent with input.

AffineTranslate()

AffineTranslate(Vector,List,Output2D=false)

  • Vector, an openSCAD translate() vector [x,y,z].

  • List, an array of vertices or a single vertex.

  • Output2D, force 2D output, even with 3D input, i.e., crop the Z-coordinate.

Perform affine transformation on an array of vertices. Returns 3D or 2D consistent with input.

This is somewhat nonsensical, you could simply use ArrayAdd() instead, but it’s here for the sake of consistency…​

AffineTransform()

AffineTransform(Matrix,List,Output2D=false)

  • Matrix, affine transformation matrix. This is an 'enhanced' 4x4 matrix containing all required transformations, see the routines below.

  • List, a single vertex or an array of vertices to be transformed. List can contain either 2D or 3D vertices; the output will be conform with the (first) vertex of the input.

  • Output2D, Boolean, output array will be cropped to 2D [X,Y] coordinates, even when the input is in 3D; used when a 2D input array needs to remain 2D.

AffineTransform() can translate, rotate, even scale or shear (skew) an entire 'cloud' of vertices, like a mesh to form a polyhedron, through 3D space. The GHOUL has several routines to create the desired 'augmented' affine transformation matrices required to do so—​see below. AffineTransform() is the 'universal' performer here, since most transformations are a combination of rotation, translation and scaling, which this routine manages with the help of TransformMatrix(), see below.

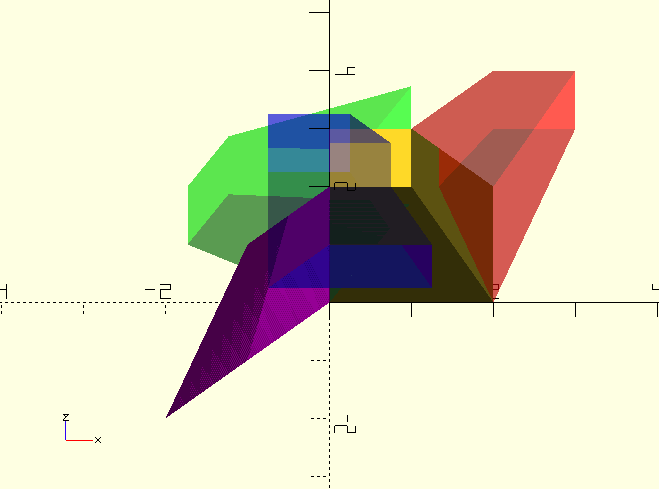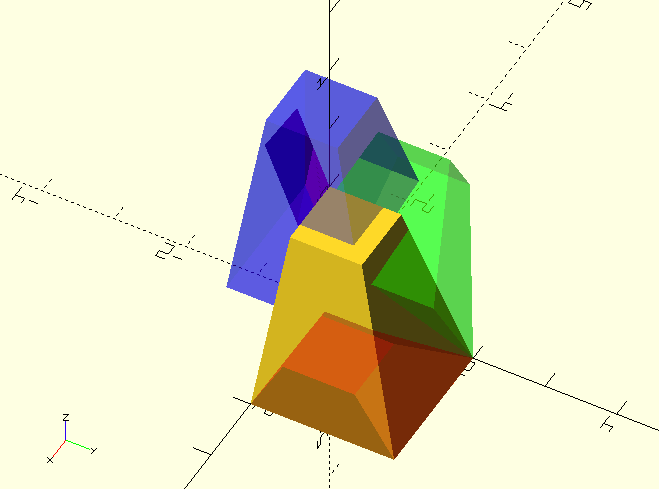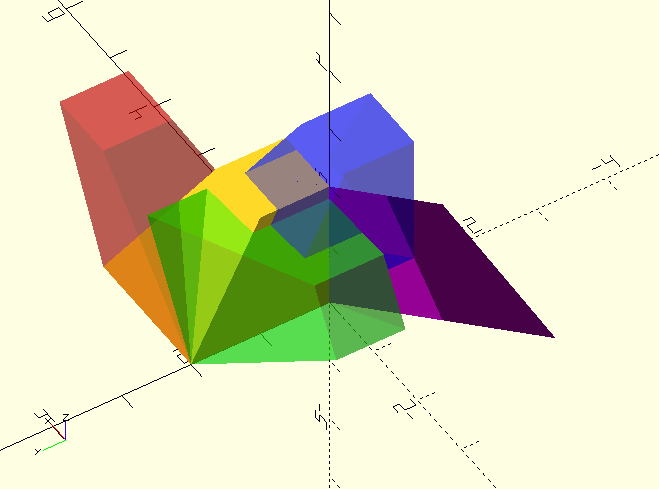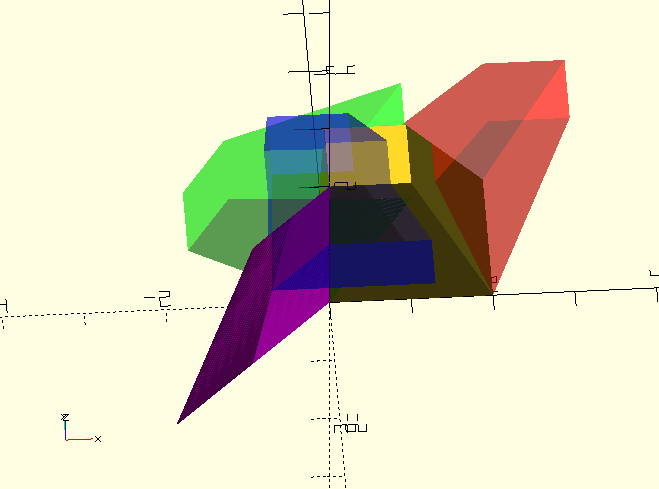
TransformMatrix

Supporting actors

HomogeniseMatrix()

HomogeniseMatrix(Matrix)

  • Matrix, a matrix of maximum dimension 4x4.

Turns any matrix (even an empty one []) into a homogenised 4x4 matrix. Used by The GHOUL’s the affine transformation routines.

echo(HomogeniseMatrix([[1,2],[3,4]]));

ECHO: [[1, 2, 0, 0], [3, 4, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]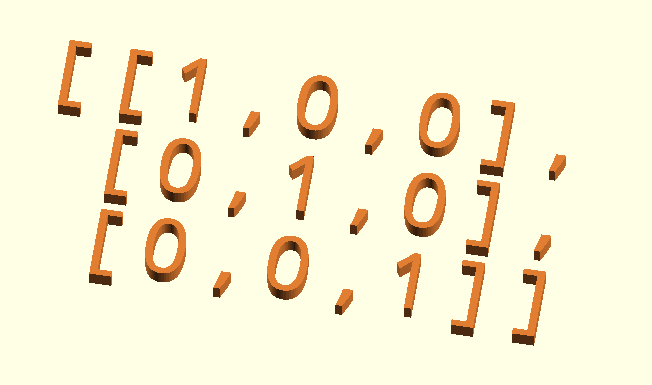

IdentityMatrix

IdentityMatrix()

IdentityMatrix(Size)

  • Size, integer, size of the matrix

IdentityMatrix() generates an identity matrix of the required size.

echo(IdentityMatrix(3));

ECHO: [[1,0,0],[0,1,0],[0,0,1]]

MatrixTranspose

MatrixTranspose()

MatrixTranspose(Matrix)

  • Matrix, matrix.

MatrixTranspose() takes matrix A and returns matrix AT, the transpose.

Foo=MatrixTranspose(
    [[11,12,13],
     [21,22,23],
     [31,32,33]]
    );
    =>
echo(Foo);

// Edited for clarity.
ECHO: [[11, 21, 31],
       [12, 22, 32],
       [13, 23, 33]]

Matrices

RotationMatrix

RotationMatrix()

RotationMatrix(Vector=[0,0,0],Angle=undef)

  • Vector, vector, rotation axis like in the OpenSCAD native rotate(a = deg_a, v = [x, y, z]). If Angle is not specified, Vector is treated as a vector of Euler angles in degrees similar to OpenSCAD rotate([x,y,z]).

  • Angle, scalar, rotation angle.

RotationMatrix() returns an affine rotation matrix. Just like the native OpenSCAD rotate() it accepts either Euler angles or a rotation axis in the form of a vector plus a rotation angle.

echo(RotationMatrix([30,45,0]));

// Echo output has been 'prettyfied'
ECHO: [
        [ 0.707, 0.353,  0.612, 0],
        [ 0    , 0.866, -0.5  , 0],
        [-0.707, 0.353,  0.612, 0],
        [ 0    , 0    ,  0    , 1]
      ]

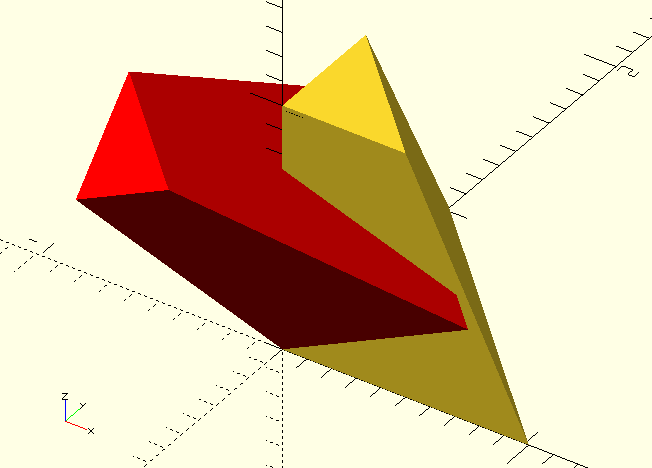
VertsA=[[0,0,0],[1,0,0],[0,1,0],[0,0,1],[0.5,0,1],[0,0.5,1]];
Faces=[[0,1,2],[0,1,4,3],[1,2,5,4],[2,0,3,5],[3,4,5]];

VertsB=AffineTransform(RotationMatrix([1,-1,0],45),VertsA);

polyhedron(VertsA,Faces);
color(RED)
polyhedron(VertsB,Faces);

/*
  Yes, we could have just done:

  rotate(45,[1,-1,0])
  polyhedron(VertsA,Faces);

  But that's not what we're here to see...
*/

ScalingMatrix

ScalingMatrix()

ScalingMatrix(Vector)

  • Vector, vector, [X,Y,Z] scaling vector like OpenSCAD scale([x,y,z]).

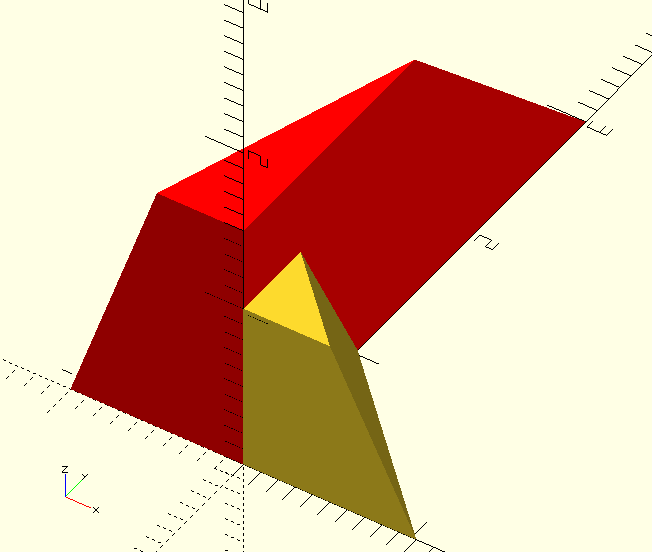
ScalingMatrix() returns an affine scaling matrix, negative scaling factors are equivalent to 'mirror' operations.

In this and the next source code examples the polyhedron definitions are the same as in the RotationMatrix() entry and are therefore omitted.

VertsB=AffineTransform(ScalingMatrix([-1,3,1.5]),VertsA);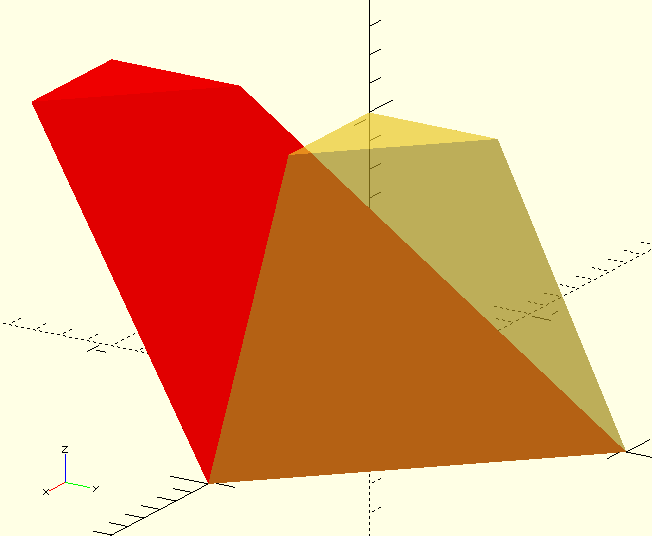

ShearingMatrix

ShearingMatrix()

ShearingMatrix(Matrix)

  • Matrix, matrix, movements along the shear axes, expressed in matrix-like form.

[
  [1,x/y,x/z],
  [y/x,1,y/z],
  [z/x,z/y,1]
]`

The parameters of the input Matrix, e.g. x/z should be read as "units of shear 'movement' along the X-axis per unit of Z-dimension". The numerator indicates the direction of the shear and the denominator indicates the dimension along which the shear takes place.
To move the top of a polyhedron with a height of 2 units 1 unit in the positive X-direction, x/z must be shear/dimension or 1/2.
To move the positive Y-end of a 3 unit long object 0.5 unit down, the z/y parameter must be -0.5/3 or -1/6 or -0.1666…​

Note Shearing can do funny things, especially when mixed with scaling and the values of two rows of the input Matrix become of the same magnitude, for example, when Matrix.x is [-1,0.5,0] and Matrix.y is [-1,0.5,0], the object becomes a plane (see TransformMatrix() below). 
VertsB=AffineTransform(ShearingMatrix(Matrix=[[1,0,0],[0,1,-1],[0,0,1]]),VertsA);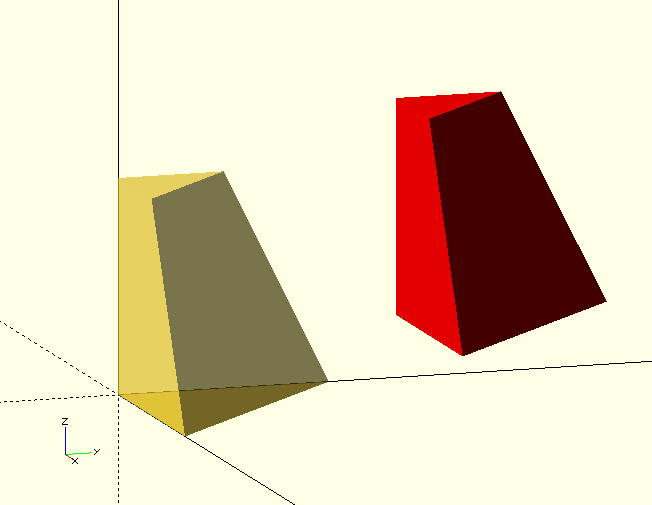

TranslationMatrix

TranslationMatrix()

TranslationMatrix(Vector)

  • Vector, vector, [X,Y,Z] translation vector like OpenSCAD translate([x,y,z]).

TranslationMatrix() returns an affine translation matrix. This one is taking things a bit far, and only makes sense when you’re combining a number of transformations (see the next entry), because used by itself, it can simply be replaced with ArrayAdd(Array,Vector).

VertsB=AffineTransform(TranslationMatrix([1,1,0.5]),VertsA);

TransformMatrix()

TransformMatrix(Transforms=[])

  • Transforms, array, an array of one or more GHOUL Transform definitions.

TransformMatrix() generates a transformation matrix from The GHOUL’s Transforms to be used by AffineTransform() or the native multmatrix(). It accepts The GHOUL’s Transform format for input, greatly facilitating the use of multiple combined transformations.

The GHOUL’s Transform inputs can be combined in an array and are processed left-to-right. Most individual Transform formats look like regular OpenSCAD inputs for transformations, with an added string element to identify the different operations. They are:

Translation

[10,3,0,"T"] — X-Y-Z units of translation, followed by "T".
Rotation

[30,0,0,"R"] — X-Y-Z degrees of rotation, followed by "R".
Scaling

[1,1,2,"S"] — X-Y-Z factors of scaling, followed by "S".
Shear

[[1,0,1/6],[0,1,0],[0,0,1],"SH"] — a shear matrix input as used by ShearingMatrix(), followed by "SH".
Combined in an array

[[30,0,0,"R"],[10,3,0,"T"]]

Have a look at the examples in the code below, pay close attention to the shape in purple. It all relates to the image above.

module DCube(){
    linear_extrude(height=2,scale=[0.5,0.5])
    square([2,2]);
}

DCube();

color(RED,0.4)
multmatrix(TransformMatrix([[[1,0,1],[0,1,0.5],[0,0,1],"SH"]]))
DCube();

// Funky 'identical row' result from shearing and scaling mix, see 'echo' below.
color(PRP)
multmatrix(TransformMatrix([[[1,-0.5,0],[-2,1,0],[0,0,1],"SH"],[-1,0.5,1,"S"]]))
DCube();

Echo(TransformMatrix([[[1,-0.5,0],[-2,1,0],[0,0,1],"SH"],[-1,0.5,1,"S"]]));
// ECHO: [-1, 0.5, 0, 0][-1, 0.5, 0, 0][0, 0, 1, 0][0, 0, 0, 1]
// Notice in the 'echo' that the 'X' and 'Y' rows of the combined shearing and scaling matrices are identical.

color(GRN,0.4)
multmatrix(TransformMatrix([[0,-60,0,"R"]]))
DCube();

color(BLU,0.4)
multmatrix(TransformMatrix([[-0.75,-0.75,1,"T"]]))
DCube();